 |  |  |
恾椺1丂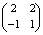 偵傛傞曄姺 偵傛傞曄姺 | 恾椺2丂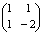 偵傛傞曄姺 偵傛傞曄姺 | 恾椺3丂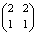 偵傛傞曄姺 偵傛傞曄姺 |
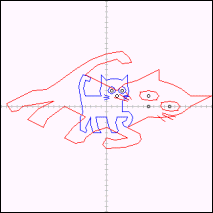
丂偝偰峴楍偑崅峑悢妛偵搊応偟偨弶傔偰偺擭丆峴楍偺帩偮堄枴偲偐侾師曄姺側偳偲偄偆懆偊偳偙傠偺側偄戣嵽偵懳偟偰朙偐側僀儊乕僕傪梌偊傞偙偲偼偱偒側偄偐偲尰応偱偺柾嶕偑懕偄偰偄偨丅偙偺傛偆側攚宨偺傕偲偱乽擫偺奊幨偟乿偑彫戲寬堦愭惗偵傛偭偰敪昞偝傟偨丅
 |  |  |
恾椺1丂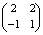 偵傛傞曄姺 偵傛傞曄姺 | 恾椺2丂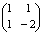 偵傛傞曄姺 偵傛傞曄姺 | 恾椺3丂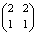 偵傛傞曄姺 偵傛傞曄姺 |
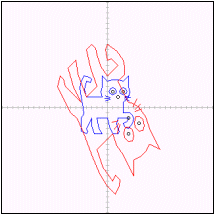
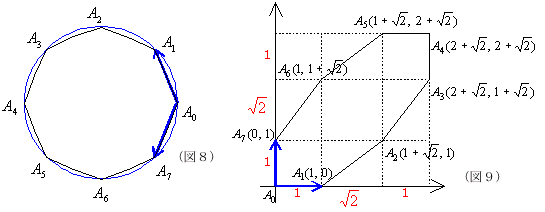
丂恾椺侾偑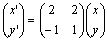 偵傛偭偰幨偝傟偨擫偱偁傞丅擫偼庒姳偮傇傟傞偑丆偟偐偟嵞傃擫偵側偭偰偄傞偙偲偑暘偐傞丅偝傜偵恾椺俀丆恾椺俁傪徯夘偡傞丅
偵傛偭偰幨偝傟偨擫偱偁傞丅擫偼庒姳偮傇傟傞偑丆偟偐偟嵞傃擫偵側偭偰偄傞偙偲偑暘偐傞丅偝傜偵恾椺俀丆恾椺俁傪徯夘偡傞丅
丂侾師曄姺偼慄宆惈偲偄傢傟傞惈幙傪帩偭偰偄傞丅偙偺惈幙偼擫幨偟偱偄偊偽丆
丂丂丂仜尨揰偼摦偐側偄
丂丂丂仜捈慄偼捈慄偵堏傞
丂丂丂仜捈慄忋偺慄暘偺挿偝偺斾偼幨偭偨偁偲傕曐偨傟傞
側偳偲偄偆恾宍忋偺惈幙偲偟偰尰傟傞丅偙傟偑丆偮傇傟偨傝夞揮偟偨傝偟偰傕壗偲偐擫偺宍傪曐偮棟桼偱偁傞丅傕偭偲傕恾椺俁偺応崌偼姰慡偵偮傇傟偰偟傑偄擫偼慄暘忬懺偵側偭偰偟傑偭偰偄傞丅偳偺傛偆側偮傇傟曽傪偡傞偐偼丆傕偪傠傫曄姺幃偵傛傞丅摿偵曄姺偺峴楍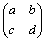 偲偺娭學偼師偺傛偆偵側偭偰偄傞丅
偲偺娭學偼師偺傛偆偵側偭偰偄傞丅
丂峴楍幃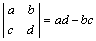 傪儮偲偡傞偲偒
傪儮偲偡傞偲偒
丂丂(1)儮亜侽側傜偽塃岦偒偺擫偵側傞
丂丂(2)儮亙侽側傜偽嵍岦偒偵側傞
丂丂(3)儮亖侽側傜偽慄暘忬懺偵偮傇傟偰偟傑偆
丂丂(4)乥倎倓亅倐們乥偑奼戝棪傪昞偡
丂埲忋堦晹暘傪彍偄偰堷梡偝偣偰捀偄偨丅偙偺乬擫乭偼悢妛嫵堢偵戝偒側塭嬁傪梌偊丆傗偑偰乽悢妛僙儈僫乕乿偺昞巻傪忺偭偨傝嫵壢彂偵婄傪弌偟偨傝偟偨丅
丂崅峑偵偍偗傞慄宆戙悢傊偺庢傝慻傒偲偟偰偼丆埲忋偺傛偆側惈幙傪偄傠偄傠側宍偱挷傋妛廗偟偰偒偨偲偄偭偰傛偄偱偁傠偆丅
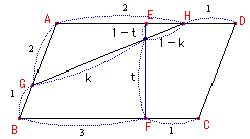 乮椺戣侾乯暯峴巐曈宍俙俛俠俢偵偍偄偰俙俛傪俀丗侾偵撪暘偡傞揰傪俧丆俛俠傪俁丗侾偵撪暘偡傞揰傪俥丆俢俙偺拞揰媦傃俢俙傪侾丗俀偵撪暘偡傞揰傪俤丆俫偲偡傞丅偄傑俧俫偲俤俥偲偺岎揰傪俬偲偡傞偲偒丆
乮椺戣侾乯暯峴巐曈宍俙俛俠俢偵偍偄偰俙俛傪俀丗侾偵撪暘偡傞揰傪俧丆俛俠傪俁丗侾偵撪暘偡傞揰傪俥丆俢俙偺拞揰媦傃俢俙傪侾丗俀偵撪暘偡傞揰傪俤丆俫偲偡傞丅偄傑俧俫偲俤俥偲偺岎揰傪俬偲偡傞偲偒丆 傪
傪 偲
偲 偲偱昞傢偣丅
偲偱昞傢偣丅
丂偁傝傆傟偨栤戣偱偁傞偑師偺傛偆側夝偒曽偑惓摑揑側傕偺偲傒側偝傟偰偄傞夝朄偱偁傠偆丅
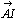 亖俀/俁(侾亅k)
亖俀/俁(侾亅k)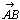 亄俀倠/俁
亄俀倠/俁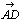 丆
丆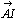 亖(侾亅倲)
亖(侾亅倲)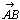 亄(俁/係亅倲/係)
亄(俁/係亅倲/係)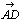
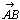 亄俀倠/俁
亄俀倠/俁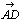 亖(侾亅倲)
亖(侾亅倲)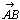 亄(俁/係亅倲/係)
亄(俁/係亅倲/係)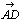 丂傛傝
丂傛傝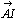 亖俀/侾俆
亖俀/侾俆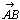 亄俉/侾俆
亄俉/侾俆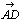
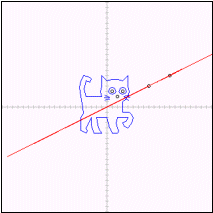
丂師偵偪傚偭偲偟偨曽朄偱夝偄偰傒傛偆丅傑偢乮恾係乯傪傕偲偵偟偰(恾俆)傪嶌傞丅
丂(恾俆)傛傝 亖乮侾丆侽乯丆
亖乮侾丆侽乯丆 亖乮侽丆侾乯丆捈慄GH偺曽掱幃偼倷亖亅倶亄俀/俁丆捈慄俤俥偺曽掱幃偼倷亖倶/係亄侾/俀丆捈慄俧俫偲捈慄俤俥偺岎揰俬偼倶亖俀/侾俆丆倷亖俉/侾俆傛傝俬(俀/侾俆丆俉/侾俆)偲側傞丅偙傟傪傕偲偵偟偰丆
亖乮侽丆侾乯丆捈慄GH偺曽掱幃偼倷亖亅倶亄俀/俁丆捈慄俤俥偺曽掱幃偼倷亖倶/係亄侾/俀丆捈慄俧俫偲捈慄俤俥偺岎揰俬偼倶亖俀/侾俆丆倷亖俉/侾俆傛傝俬(俀/侾俆丆俉/侾俆)偲側傞丅偙傟傪傕偲偵偟偰丆
丂丂丂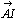 亖(俀/侾俆丆俉/侾俆)亖俀/侾俆(侾丆侽)亄俉/侾俆(侽丆侾)
亖(俀/侾俆丆俉/侾俆)亖俀/侾俆(侾丆侽)亄俉/侾俆(侽丆侾)
丂丂丂丂亖俀/侾俆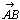 亄俉/侾俆
亄俉/侾俆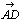
丂愭掱儀僋僩儖偺侾師撈棫惈傪傕偲偵偟偰夝偄偨傕偺偲摨偠夝摎偑摼傜傟傞偺偱偁傞丅偙傟偼嬼慠偺堦抳偱偼側偔丆侾師撈棫惈偵怺偔崻偞偟偨夝朄側偺偱偁傞丅(恾係)偲(恾俆)偲偼慡偔堘偭偨恾側偺偱偁傞丅偦傟側偺偵(恾俆)傪傕偲偵偟偰摫偄偨夝摎偑(恾係)偺夝摎偲傒側偟偰傛偄偲偼擛壗側傞崻嫆偵傕偲偯偔傕偺側偺偐丅(恾係)偲(恾俆)偲傪拲堄怺偔斾妑偟偰傒傞偲(恾係)偱暯峴側慄暘偳偆偟偼(恾俆)偱傕暯峴偲側偭偰偄傞丅傑偨(恾係)偱偺摨堦捈慄忋埥偼暯峴側捈慄忋偱偺慄暘斾偼(恾俆)偺忋偱傕曐偨傟偰偄傞丅偮傑傝(恾係)偲(恾俆)偲偼侾師曄姺偺廳梫惈幙偵傕偲偯偄偰(恾係)偑(恾俆)偵堏偭偰偄偭偨偲峫偊傞偙偲偑偱偒丆傑偨偦偺傛偆側侾師曄姺倖偼昁偢懚嵼偡傞偺偱偁傞丅偦偟偰偙偺侾師曄姺倖偼昁偢媡曄姺倖-1偑懚嵼偡傞傛偆側倖側偺偱偁傞丅偟偐偟(恾係)偲(恾俆)偺娭學偱偼侾師曄姺偺幃昞尰偼堦愗昞偵偼弌偰偄側偄丅偦偺戙傝偵(恾係)偐傜(恾俆)傪彂偄偰備偔拞偱変乆偼侾師曄姺倖傪乬幚峴乭偟偰偄傞偺偱偁傞偲偄偭偰傛偄偱偁傠偆丅偦偟偰(恾係)偲偼尨憸偱偁傝丆(恾俆)偼憸側偺偱偁傞丅尨憸偲憸偲偺娭學偵偍偄偰儀僋僩儖偺娭學幃偼侾師曄姺偵傛偭偰曄傢傜側偄偐傜(恾俆)偵偍偗傞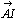 傪昞傢偡幃偼(恾係)偵偍偄偰傕摨偠娭學偱昞偝傟傞偙偲偵側傞偺偱偁傞丅偙偺夝朄偱偼侾師曄姺偼昞偵偼弌偰偙側偄偑丆夝朄偺掙棳傪巟偊傞廳梫棟榑偱偁傞偙偲偼曄傢傜側偄丅惔悈愭惗偑侾師曄姺傪倀俥俷偲柤偯偗丆偙偺傛偆側夝朄傪倀俥俷嶌愴偲柤偯偗偨偺偼幚偵偡偽傜偟偄柦柤偱偁傞偲巚偆偺偼巹堦恖偩偗偱偁傠偆偐丅
傪昞傢偡幃偼(恾係)偵偍偄偰傕摨偠娭學偱昞偝傟傞偙偲偵側傞偺偱偁傞丅偙偺夝朄偱偼侾師曄姺偼昞偵偼弌偰偙側偄偑丆夝朄偺掙棳傪巟偊傞廳梫棟榑偱偁傞偙偲偼曄傢傜側偄丅惔悈愭惗偑侾師曄姺傪倀俥俷偲柤偯偗丆偙偺傛偆側夝朄傪倀俥俷嶌愴偲柤偯偗偨偺偼幚偵偡偽傜偟偄柦柤偱偁傞偲巚偆偺偼巹堦恖偩偗偱偁傠偆偐丅
乮椺戣俀乯惓榋妏宍俙俛俠俢俤俥偵偍偄偰俠俢傪侾丗俀偺斾偵撪暘偡傞揰傪俧偲偡傞丅俙俧偲俛俥偺岎揰傪俹偲偡傞偲偒丆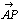 傪
傪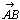 偲
偲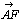 偱昞傢偣丅
偱昞傢偣丅
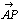 亖乮侾亅倠乯
亖乮侾亅倠乯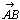 亄倠
亄倠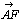 丂乧嘆
丂乧嘆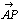 亖倲
亖倲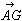 亖倲(
亖倲(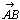 亄
亄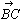 亄
亄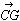 )
)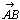 亄
亄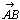 亄
亄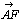 亄侾/俁
亄侾/俁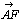 )亖倲(俀
)亖倲(俀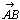 亄係/俁
亄係/俁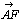 )
)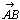 亄係倲/俁
亄係倲/俁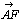 丂乧嘇
丂乧嘇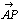 亖俁/俆
亖俁/俆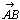 亄俀/俆
亄俀/俆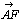
丂師偵(恾7)傪傕偲偵偟偰夝偄偰傒傛偆丅
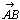 亖(俁/俆丆俀/俆)亖俁/俆(侾丆侽)亄俀/俆(侽丆侾)亖俁/俆
亖(俁/俆丆俀/俆)亖俁/俆(侾丆侽)亄俀/俆(侽丆侾)亖俁/俆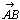 亄俀/俆
亄俀/俆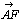
丂壗偲傕晄巚媍側夝朄偱偼偁傞丅(恾俇)偼惓榋妏宍偱偁傞偑(恾俈)偵帄偭偰偼惓榋妏宍偱偼側偄偺偱偁傞丅偦傟偱偄偰惓榋妏宍偵娭偡傞栤戣傪夝偔偙偲偑偱偒傞偺偼(恾俇)傪尨憸丆(恾俈)傪徾偲偡傞侾師曄姺倖偑懚嵼偟丆憸傪傕偲偵偟偰媮傔傜傟偨 偺幃偼媡曄姺倖-1偵傛偭偰尨憸偵偍偄偰傕惉傝棫偮娭學幃偱偁傞偲傒側偡偙偲偑偱偒傞偐傜側偺偱偁傞丅巹偼尨憸偲偟偰偺恾傪(尦恾)丆徾偲偟偰偺恾傪(怴恾)偲屇傃丆惓榋妏宍偑侾師曄姺偵傛偭偰僨僼僅儖儊偝傟偰偱偒傞榋妏宍傪乬曄恎榋妏宍乭偲屇傫偱偄傞丅
偺幃偼媡曄姺倖-1偵傛偭偰尨憸偵偍偄偰傕惉傝棫偮娭學幃偱偁傞偲傒側偡偙偲偑偱偒傞偐傜側偺偱偁傞丅巹偼尨憸偲偟偰偺恾傪(尦恾)丆徾偲偟偰偺恾傪(怴恾)偲屇傃丆惓榋妏宍偑侾師曄姺偵傛偭偰僨僼僅儖儊偝傟偰偱偒傞榋妏宍傪乬曄恎榋妏宍乭偲屇傫偱偄傞丅
丂偦偙偱惓榋妏宍偵娭偡傞栤戣偼丆傑偢偁傜偐偠傔乬曄恎榋妏宍乭偲偟偰(恾俈)偺榋妏宍俙俛俠俢俤俥傪擮摢偵偍偔偲偒丆栤戣偵墳偠偰娙扨側惉暘寁嶼偲偟偰張棟偟偰偟傑偆偙偲偑偱偒傞偺偱偁傞丅埲忋(椺戣侾乯傗(椺戣俀)偺曽朄偼惔悈愭惗偺憂埬偵傛傞傕偺偱偁傞偑丆懡偔偺庴尡惗偑偙偺夝朄偵愙偟偰備偔偆偪偵儀僋僩儖傊偺嬯庤堄幆傪夝徚偟偰偄偭偨偺偱偁偭偨丅
丂巹偺慜擟峑(嶥杫搶崅峑)偱傕庼嬈傗庴尡懳嶔偺島嵗偱偙偺曽朄傪愊嬌揑偵巜摫偟偰偒偨偺偱偁偭偨丅偑偦偺偆偪偵巹偼惗搆偺幙栤偵擸傓偙偲偵側偭偨丅偦偺幙栤偲偼栤戣傪恀寱偵峫偊傞庴尡惗側傜摉慠書偔偱偁傠偆媈栤偱偁偭偨丅斵摍偼惓敧妏宍偺栤戣傪倀俥俷嶌愴偱夝偔偨傔偵偼偳傫側恾傪彂偄偰峫偊偨傜傛偄偺偐偲幙栤偟偰偒偨偺偱偁傞丅拞偵偼惓廫擇妏宍偺栤戣傪帩偭偰偒偰丆偙傟傪倀俥俷嶌愴偱夝偒偨偄偺偩偗傟偳傕偳傫側恾傪彂偄偨傜傛偄偺偐嫵偊偰傎偟偄偲偄偆偺傕偁偭偨丅嬯偟暣傟偵偄偔偮偐偺恾傪彂偄偰搉偟偨傝偟偨偺偱偁偭偨偑岾偄側偙偲偵偡傋偰偺恾偱惓夝偵払偡傞偺偱偁偭偨丅偦偺傛偆側栤戣傪傆傝偐偊偭偰傒傛偆丅
乮椺戣俁乯惓敧妏宍俙0俙1俙2俙3俙4俙5俙6俙7偵偍偄偰丆 亖
亖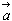 丆
丆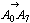 亖
亖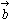 丂偲偡傞丅
丂偲偡傞丅
丂(1)師偺儀僋僩儖傪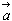 丆
丆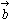 傪梡偄偰昞傢偣丅
傪梡偄偰昞傢偣丅
丂丂丂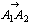 亖(丂丂丂)
亖(丂丂丂)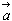 亄
亄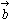 丆丂丂
丆丂丂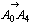 亖(丂丂丂)(
亖(丂丂丂)(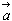 亄
亄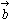 )
)
丂(2)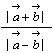 亖(丂丂丂)
亖(丂丂丂)
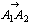 亖(侾亄併俀丆侾)亅(侾丆侽)亖(併俀丆侾)
亖(侾亄併俀丆侾)亅(侾丆侽)亖(併俀丆侾) 亄
亄
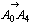 亖(俀亄併俀丆俀亄併俀)亖俀亄併俀(侾丆侾)
亖(俀亄併俀丆俀亄併俀)亖俀亄併俀(侾丆侾)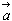 亄
亄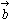 )
)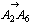 亖(侾丆侾亄併俀)亅(侾亄併俀丆侾)亖(亅併俀丆併俀)
亖(侾丆侾亄併俀)亅(侾亄併俀丆侾)亖(亅併俀丆併俀)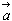 亅
亅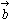 )
)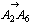 乥亖乥
乥亖乥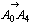 乥丂偱偁傞偐傜
乥丂偱偁傞偐傜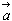 亄
亄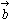 乥亖併俀乥
乥亖併俀乥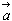 亅
亅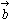 乥
乥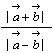 亖併俀亅1
亖併俀亅1丂偝偰偙偺傛偆偵(恾俋)傪傕偲偵偟偰惓敧妏宍偵娭偡傞栤戣傪夝偔偙偲偑偱偒傞偺偩偑丆堦斒偵惓懡妏宍傪侾師曄姺偵傛偭偰幨偡偲偒偳偺傛偆側僨僼僅儖儊偝傟偨懡妏宍偑偊傜傟傞偺偐丆偦偺偙傠偼傛偔敾傜側偐偭偨丅惓懡妏宍俙0俙1俙2丒丒丒俙n-1偵偍偄偰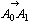 偲
偲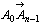 偲傪婎掙偲偡傞丅侾師曄姺偵傛偭偰
偲傪婎掙偲偡傞丅侾師曄姺偵傛偭偰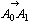 偑(侾丆侽)偵丆
偑(侾丆侽)偵丆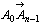 偑乮侽丆侾乯偵幨傞偲偒偵懠偺俙0俙1俙2丒丒丒俙n-1偲偄偆揰偼偳偺傛偆側揰偵幨偭偰備偔偺偱偁傠偆偐偲偄偆栤戣傪夝寛偡傟偽傛偄偺偩偑丆偦傟偑側偐側偐傛偄峫偊偑弌偰偙側偄偱擸傫偩偙偲傕偁偭偨偺偱偁傞丅
偑乮侽丆侾乯偵幨傞偲偒偵懠偺俙0俙1俙2丒丒丒俙n-1偲偄偆揰偼偳偺傛偆側揰偵幨偭偰備偔偺偱偁傠偆偐偲偄偆栤戣傪夝寛偡傟偽傛偄偺偩偑丆偦傟偑側偐側偐傛偄峫偊偑弌偰偙側偄偱擸傫偩偙偲傕偁偭偨偺偱偁傞丅
丂埲忋偺栤戣偵柧夝側夝寛傪摼偨偺偼偦偆愄偺偙偲偱偼側偄丅嶐擭偺擔悢嫵嶳岥戝夛偵偍偄偰丆堦墳偺惉壥傪敪昞偝偣偰捀偄偨偑丆悢幚尋偺乽悢妛偺偄偢傒乿偺拞偵傕乬惓懡妏宍偺曄恎乣偍傕偟傠偄僨僼僅儖儊乭偲偟偰愘暥偍偝傔偰捀偄偨丅偦偙偱巻柺偱偼偙傟埲忋尵媦偡傞昁梫偼側偄偲巚偆偺偩偑丆惓懡妏宍偺曄恎偵偮偄偰柧夝側尒捠偟偑摼傜傟偨偙偲偵傛偭偰儀僋僩儖偺倀俥俷埆愴偼擖帋栤戣夝朄偲偟偰姰慡側棟榑偲側偭偨偲偄偊傞偺偩偲巹偼巚偆偺偩丅
丂偟偐偟丆惔悈愭惗傕巹傕擖帋栤戣偺夝朄偲偄偆榞偺拞偱丆憸傪捠偟偰尨憸傪抦傞偲偄偆敪憐傪幚慔偟偰偒偨偺偱偁傞丅崱夞偺拞懞愭惗偺儗億乕僩偼擖帋栤戣偺榞傪棧傟偰恾宍偺曄恎偵敆傠偆偲偟偰偄傞丅偙偺傛偆側怴偟偄敪憐偺拞偐傜朙偐側悽奅偑傂傜偗偰偔傞偐傕偟傟側偄丅偦偺傛偆側婜懸傪偦偙偼偐偲側偔桸偒弌偝偣傜傟傞儗億乕僩偱偁傞偲姶偠偨丅
丂偁偲偼偛杮恖偵岅偭偰捀偔偙偲偵偟傛偆丅