しかし、ｘ2＝−４となるｘは、実数の範囲内では存在しないのであるから、実数の解のみが方程式の解であると意識されている場合には“この方程式には解がない”といってもよい訳である。
従って√−４とか２ｉなどを書いても、これはあくまでも仮空の数であって只形式的に計算する記号に過ぎないとも言えるのである。２次方程式を解くという立場だけで考えるならば虚数を新しい数と見なす必然性はないともいえる。ところが、３次方程式の解法の研究が進むにつれて奇妙な事実が判ってきた。
ｘ3＋ａｘ＝ｂの型の３次方程式は
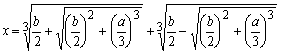
を解にもつことが１６世紀初頭に発見された。
今ｘ3−１８ｘ＝８にこの公式を適用してみよう。
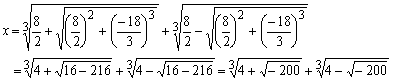
となり√−２００を合む記号で表わされる数である。
ところでこの方程式を因数分解法で解いてみよう。
ｘ3−１８ｘ＝８よりｘ3−１８ｘ−８＝０
∴ (ｘ＋４)(ｘ2−４ｘ−２)＝０
となり
ｘ＝−４、２±√６
となる。
ｘ＝−４、２＋√６、２−√６はいずれも実数であるから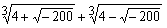
は実数であると認めなければならないであろう。
つまり“れっきとした”実数が“仮空”の√−２００等を媒介として表現されているのである。
このような研究が進むにつれて、１８世紀頃には虚数は新しい数として認知されていた。仮空の数が、新しい数としての市民権を獲得していたのである。