幚悢倎丄倐偺弴彉懳乮倎丄倐)傪峫偊傞丅偙傟傪暋慺悢偲屇傃偦偺憡摍丄榓丄愊傪師偺傛偆偵掕媊偡傞丅丂(俀)丄(俁)偱偺嵍曈偺
(侾)(倎丄倐)亖(們丄倓)偺偲偒倎亖們偐偮倐亖倓
(俀)(倎丄倐)(們丄倓)亖(倎亄們丄倐亄倓)
(俁)(倎丄倐)(們丄倓)亖(倎們亅倐倓丄倎倓亄倐們)
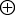 丄
丄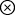 偼怴偟偔掕媊偡傞暋慺悢偺榓丄愊傪昞傢偡婰崋偲偄偆堄枴偱偁傝丄塃曈
偼婛偵抦傜傟偰偄傞幚悢偺悽奅偱偺巐懃偱偁傝丄崱偙傟傜傪嬫暿偟偰昞偟偰偍偙偆偲偟偰偄傞偺偱
偁傞丅
偼怴偟偔掕媊偡傞暋慺悢偺榓丄愊傪昞傢偡婰崋偲偄偆堄枴偱偁傝丄塃曈
偼婛偵抦傜傟偰偄傞幚悢偺悽奅偱偺巐懃偱偁傝丄崱偙傟傜傪嬫暿偟偰昞偟偰偍偙偆偲偟偰偄傞偺偱
偁傞丅
丂(倎丄倐)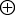 (侽丄侽)亖(侽丄侽)
(侽丄侽)亖(侽丄侽)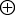 (倎丄倐)亖(倎亄侽丄倐亄侽)亖(倎丄倐)偱偁傞偐傜
(倎丄倐)亖(倎亄侽丄倐亄侽)亖(倎丄倐)偱偁傞偐傜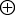 偵娭偟偰乬楇乭偺栶帺傪壥偨偡偺偑(侽丄侽)偱偁傞丅
偵娭偟偰乬楇乭偺栶帺傪壥偨偡偺偑(侽丄侽)偱偁傞丅
丂擟堄偺(倎丄倐)偵懳偟偰
丂丂丂(倎丄倐)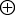 (亅倎丄亅倐)亖(侽丄侽)
(亅倎丄亅倐)亖(侽丄侽)
偲側傞偐傜丄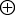 偵娭偟偰(倎丄倐)偺媡尦偑(亅倎丄亅倐)偱偁傞丅
偵娭偟偰(倎丄倐)偺媡尦偑(亅倎丄亅倐)偱偁傞丅
丂偦偙偱(倎丄倐)偲(們丄倓)偺尭朄傪(倎丄倐)偲(亅們丄亅倓)偲偺榓偲偟偰師偺傛偆偵掕媊偡傞丅
(係)(倎丄倐)丂師偵忔朄偵偮偄偰峫偊偰傒傛偆丅(們丄倓)亖(倎丄倐)
(亅們丄亅倓)亖(倎亅們丄倐亅倓)
丂丂丂(侽丄侽)
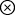 (倎丄倐)亖(倎丄倐)
(倎丄倐)亖(倎丄倐)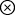 (侽丄侽)亖(侽丄侽)
(侽丄侽)亖(侽丄侽)丂丂丂(侾丄侽)
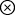 (倎丄倐)亖(倎丄倐)
(倎丄倐)亖(倎丄倐)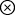 (侾丄侽)亖(倎丄倐)
(侾丄侽)亖(倎丄倐)
丂偙偺偙偲偐傜忔朄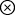 偵娭偟偰扨埵尦偲側傞偺偼(侾丄侽)偱偁傞丅擟堄偺(倎丄倐)偵懳偟偰((倎丄倐)亗(侽丄侽)偲偡傞)
偵娭偟偰扨埵尦偲側傞偺偼(侾丄侽)偱偁傞丅擟堄偺(倎丄倐)偵懳偟偰((倎丄倐)亗(侽丄侽)偲偡傞)
丂丂丂丂(倎丄倐)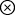 (倎/(倎2亄倐2)丄亅倐/(倎2亄倐2))亖(侾丄侽)
(倎/(倎2亄倐2)丄亅倐/(倎2亄倐2))亖(侾丄侽)
偲側傞偐傜忔朄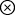 偵娭偟偰(倎丄倐)偺媡尦偼
偵娭偟偰(倎丄倐)偺媡尦偼
丂丂丂(倎/(倎2亄倐2)丄亅倐/(倎2亄倐2))
偱偁傞丅
丂偙偙偱(們丄倓)偺媡尦(們/(倎2亄倐2)丄亅倓/(倎2亄倐2))傪梡偄偰丄(倎丄倐)偲(們丄倓)偺彍朄偵偮偄偰師偺傛偆偵掕媊偡傞丅
(俆)(倎丄倐)丂埲忋偺掕媊偵婎偯偄偰師偺寁嶼傪偟偰傒傛偆丅(們丄倓)亖(倎丄倐)
(們/(倎2亄倐2)丄亅倓/(倎2亄倐2))
丂丂丂(倎丄侽)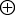 (倐丄侽)亖(倎亄倐丄侽)
(倐丄侽)亖(倎亄倐丄侽)
丂丂丂(倎丄侽) (倐丄侽)亖(倎亅倐丄侽)
(倐丄侽)亖(倎亅倐丄侽)
丂丂丂(倎丄侽)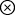 (倐丄侽)亖(倎倐丄侽)
(倐丄侽)亖(倎倐丄侽)
丂丂丂(倎丄侽)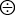 (倐丄侽)亖(倎/倐丄侽)丂(倐亗侽)
(倐丄侽)亖(倎/倐丄侽)丂(倐亗侽)
偲側傝(倎丄侽)偲偐(倐丄侽)偺宍偺暋慺悢偼巐懃寁嶼偵娭偟偰偼幚悢偺倎傗倐偲摨偠摥偒傪偟偰偄傞丅
丂偮傑傝暋慺悢(倎丄侽)偲幚悢倎偲傪摨堦帇偡傞偙偲偑壜擻偱偁傝丄(倎丄侽)傗(倐丄侽)偵偮偄偰偼丄
忋婰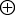 丄
丄 丄
丄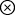 丄
丄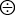 偼幚悢偺寁嶼偵偍偗傞壛尭忔彍偲摨亅帇偱偒傞偙偲傕敾傞丅崱屻偼(倎丄倧)傪扨偵倎偲彂偄偰傕傛偄帠偵側傞栿偱偁傞丅偮傑傝幚悢偽怴偟偔掕媊偝傟偨暋慺悢偺拞偺摿暿側応崌偲偟偰埵抲偯偗傜傟傞偺偱偁傞丅
偼幚悢偺寁嶼偵偍偗傞壛尭忔彍偲摨亅帇偱偒傞偙偲傕敾傞丅崱屻偼(倎丄倧)傪扨偵倎偲彂偄偰傕傛偄帠偵側傞栿偱偁傞丅偮傑傝幚悢偽怴偟偔掕媊偝傟偨暋慺悢偺拞偺摿暿側応崌偲偟偰埵抲偯偗傜傟傞偺偱偁傞丅
丂(倎丄倐)2亖(倎丄倐)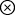 (倎丄倐)偲掕媊偟傛偆丅
(倎丄倐)偲掕媊偟傛偆丅
丂偙偺偲偒(侽丄侾)2亖(侽丄倢)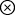 (侽丄侾)亖(亅侾丄侽)偲側傝丄偙傟偼幚悢偺亅侾傪昞偟偰偄傞丅偦偙偱(侽丄侾)傪倝偱昞傢偡偙偲偵偡傞偲倝2亖亅侾偲側傞丅擟堄偺(倎丄倐)偵偮偄偰偼(倎丄倐)亖(倎丄侽)
(侽丄侾)亖(亅侾丄侽)偲側傝丄偙傟偼幚悢偺亅侾傪昞偟偰偄傞丅偦偙偱(侽丄侾)傪倝偱昞傢偡偙偲偵偡傞偲倝2亖亅侾偲側傞丅擟堄偺(倎丄倐)偵偮偄偰偼(倎丄倐)亖(倎丄侽)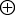 (侽丄倐)偑惉傝棫偪丄峏偵(倐丄侽)
(侽丄倐)偑惉傝棫偪丄峏偵(倐丄侽)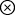 (侽丄侾)亖(侽丄倐)偲側傞偺偱(倎丄倐)亖(倎丄侽)
(侽丄侾)亖(侽丄倐)偲側傞偺偱(倎丄倐)亖(倎丄侽)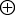 (侽丄倐)亖(倎丄侽)
(侽丄倐)亖(倎丄侽)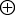 乷(倐丄侽)
乷(倐丄侽)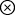 (侽丄侾)亖倎亄倐丒倝偺傛偆偵昞傢偡偙偲偑壜擻偲側傞丅
(侽丄侾)亖倎亄倐丒倝偺傛偆偵昞傢偡偙偲偑壜擻偲側傞丅
丂偮傑傝暋慺悢偺墘嶼偲偟偰憱媊偝傟偨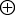 偲
偲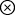 偲偱倎亄倐丒倝偺亄偲丒偲傪昞偟偰偄傞偙偲偵側傞丅
偲偱倎亄倐丒倝偺亄偲丒偲傪昞偟偰偄傞偙偲偵側傞丅
丂峏偵峫嶡傪恑傔偰備偔偲倎亄倐丒i偲彂偄偨亄傗丒偼丄徫悢偺壛朄傗忔捗偺亄丄丒偲摨堦帇偟偰傕傛 偄偙偲偑帵偝傟傞偺偱偁傞丅
丂埲忋偺傛偆側棟榑揥奐偑弴彉懳偵傛傞暋慺悢偺掕媊偱偁傞丅拪徾揑戙悢妛偺庤朄偵廗弉偟偨妛廗 幰偱側偗傟偽丄側偐側偐棟夝偡傞偵偼擄偟偄撪梕偲偄偊傛偆丅