![]() 1次変換の性質
1次変換の性質
![]() ,
,![]() を平面上のベクトル,Pを2行2列の行列とする。このとき
を平面上のベクトル,Pを2行2列の行列とする。このとき![]() となる
となる![]() を
を![]() と表わす。
と表わす。
![]() で
で![]() である。
である。
このときの写像 f については,![]() ,
,![]() が成り立つ。
が成り立つ。
f を1次変換と呼び,行列Pは1次変換f を表わす行列である。
f によって原点は原点に移る。今,点A,Bはf によってそれぞれA',B'に移るとしよう。
直線AB上の任意の点Xについては,![]() (tは実数) が成り立つ。f によってXはX'に移るとすると,
(tは実数) が成り立つ。f によってXはX'に移るとすると,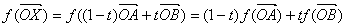 より
より![]() となる。
となる。
従って,f によって2点A,Bを通る直線はA',B'を通る直線に移る。更に点C,DはそれぞれC',D'に移るとし,![]() とする。
とする。
![]()
また,![]() ,
,
![]() ,
,
∴ ![]()
よって平行な関係にあるベクトルは,f によって移ったあとでも,それぞれまた平行な関係を保つベクトルとなっている。ここから発展して平行な関係にある線分の長さの比はf によって変わらないことがわかる。
また,同一直線上の2つの線分の比も変わらない。
![]() ,
,![]() を2辺とする三角形の周上及び内部の点Xについては
を2辺とする三角形の周上及び内部の点Xについては![]() となる。
となる。
このとき,![]() となり,
となり,![]() であるからX'は△OA'B'の周上及び内部に存在する。
であるからX'は△OA'B'の周上及び内部に存在する。
一般にf によって領域は領域へと移されていく。
△OABの面積をS,△OA'B'の面積をS'とし,f を表わす行列は![]() とする。
とする。
このとき,![]() が成り立つ。
が成り立つ。
この理論を推し進めてゆくと図形W,Vがそれぞれ図形W',V'に移るときWとVの面積の比は,W'とV'の面積の比に等しい。このことからf によって面積の比は変わらないといえる。
次に![]() が成り立つとき,f によって
が成り立つとき,f によって![]() は
は![]() ,
,![]() は
は![]() ,
,![]() は
は![]() にそれぞれ移るとする。
にそれぞれ移るとする。
![]() ,により
,により![]() となる。
となる。
f によってベクトルを表わす1次式は変わらないことがわかる。3つの点O,A,Bは一直線上にはないものとし,座標はO(0,0),A(a1,a2),B(b1,b2)とする。f によってAは(1,0)に,Bは(0,1)に移るとき,f を表わす行列Pはどのような形のものであろうか。
![]() より
より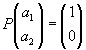
![]() より
より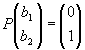
よって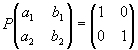 ・・・①
・・・①
O,A,Bは同一直線上にないので,a1b2-a2b1≠0,故に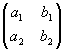 には逆行列が存在するので①の両辺に右から
には逆行列が存在するので①の両辺に右から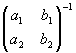 をかける。 ∴
をかける。 ∴ 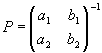
よって同一直線上にない3点O,A、B(Oは原点)をO,(1,0),(0,1)に移す f が存在する。
以上より1次変換 f の重要性質をまとめてみよう。
(1)1次変換で変わらないもの
①平行な2つの線分の比
②同一直線上の2つの線分の比
③2つの図形の面積比
④2直線が平行である性質及び交わる性質
⑤ベクトルを表わす1次式
(2)1次変換で変わるもの
①線分の長さ
②図形の面積
③2直線のなす角度
④点の座標
(3)Oを原点とすると,同一直線上にない3点O,A,BをO,(1,0),(0,1)に移す1次変換f が存在する。