基底ベクトルの変換

　平面上のあらゆるベクトルは2個の基底となるベクトルを用いて表わすことができる。この基底となるベクトルを，とし，任意の点をXとするととなる実数k ， l が存在する。

　をに，をに移す1次変換fは必ず存在するから，，とおく。この f によってXはX'に移るとき，となるから，ずべてのベクトルは，を基底とするベクトルに変換される。

　A( a ₁， a ₂)，B( b ₁， b ₂)のとき， f を表わす行列は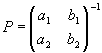であったから， f ⁻¹を表わす行列は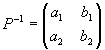である。，を基底とするベクトルは f ⁻¹により，を基底とするベクトルに移るともいえるのである。

　以上のことをベクトルの図を書き表す場合に利用してみよう。

　，を基底とした図を，を基底とした図に書き移したり，逆に，を基底とした図を，が基底の図へと書き移したりすることができる。この場合， f を表わす行列や， f ⁻¹を表わす行列を求める必要はない。 f によってベクトルを表わす1次式は不変であること，そこから同一直線上の線分比は変わらないとか，平行な2つの線分比は変わらない等などの性質をふまえて図を書いてゆけば，行列が不明でも， f にもとずいて図を書いたり，或いは f ⁻¹にもとづいて考察していることになるのである。

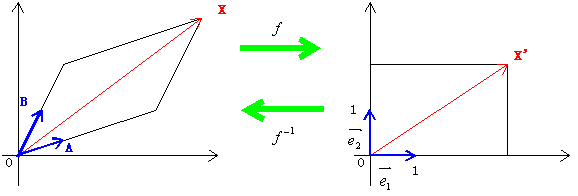
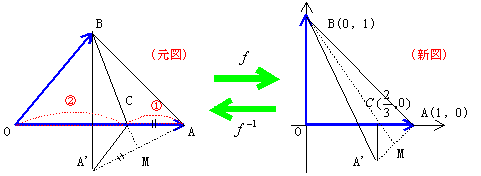
　これからの叙述の都合上，問題文の意味を書き表した図を(元図)， f によって移った状態を表わした図を(新図)となずけることにする。今，が左図の如くであるとき， f によって写された図は右図の如くになる。

　この左図を(元図)，右図を(新図)と呼ぶのである。 f により(元図)から(新図)が得られるが，逆に f ⁻¹により(新図)から(元図)が得られるのである。

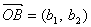　は f によって，となるのだが，これを(新図)におけるとして表わす。そして(元図)では，であるが(新図)では，として扱うのである。この方が f によってベクトルの関係式は変わらないということを強く意識することができるし，また f や f ⁻¹がわからないままでも写像そのものを意識してゆくには便利なのである。

　ここでいくつかの問題を例にして考えてみよう。

（例1） 三角形OABの紙片がある。辺OAを2：1に内分する点をCとし，線分BCを折り目として辺BAを折り返したものをBA'とすると，A'CとOBが平行になった。，とする。 (1) ＝（　　　）＋（　　　）　である。 (2) ，＋（　　　）＝ k とすると 　　t＝（　　　）， k ＝（　　　）　である。 (3) 2辺の比　OA：OB＝（　　　）：（　　　）

　(元図)において△ABA'と△ACA'は2等辺三角形である。従ってBCの延長とAA'との交点MはAA'の中点である。また題意よりOBとA'Cは平行，OA：OC＝3：2となり，以上の性質は f により変わらない。そこで(新図)ではOを原点，Aを(1，0)，Bを(0，1)とおき，Cはとおけばよいことになる。以下推論や計算は(新図)を通して行い，その結果を(元図)で解釈してゆくことにする。

(1) ，よって(元図)でもとなる。

(2) OBとA'Cが平行よりA'は直線上にある。そこでとおく。

　より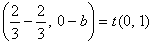　　∴ b ＝−t

　よって。このときA，A'の中点Mの座標はとなる。

　点MはBCを通る直線上にあるから　　∴

　またより，

　　∴　　より　

(3) (新図)より。この関係は(元図)においても同じであるからA'C：OB＝1：2。

　　よって(元図)でOB＝2A'C，OA＝3CA＝3A'C　　∴ OA：OB＝3A'C：2A'C＝3：2

（例2）△OABに対し，とする。実数 m ，n が m ≧0，n ≧0，2m+3n≦6を満たす点Xの存在範囲を図示せよ。

　(元図)でのXの存在範囲を求めるのであるが，まず(新図)で点Xの存在範囲を求める。

　，m≧0，n≧0，2m+3 n≦6･･･�@。この�@は(新図)でも成り立っている。いま(新図)で点Xの座標は(x，y)とするとより(x，y)＝m(1，0)+n(0，1)=(m，n )　∴x=m ，y=n ･･･�A

　�Aを�@に代入して，x≧0，y≧0，2x+3y≦6

　　∴ ･･･�B　　よって(新図)でXの存在範囲は図の如くなる。

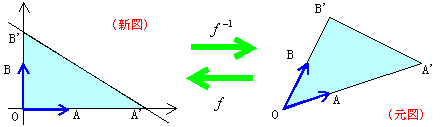
　この(新図)で

　　，

となり，点Xは△OA'B'の周上及び内部に存在する。これは(元図)においても成り立つ関係である。