（例１）バクテリアはある一定の条件のもとでは，一定時間にａ分裂する。（1個のバクテリアがａ個に分裂するという意味である)。つまり単位時間毎に何倍かずつになっていくことをくり返す。

（例２）放射性元素の原子の個数は時間が経過すると共に減少していく。1秒たてば前の１/ａとなるという実験法則がある。

（例３）ガラスのような透明な媒質を通る光は，この媒質に少しずつ吸収されていく。従って媒質の中を進めば進む程そこを通る光の量は吸収され続け次第に減少してゆく。
実験法則によるとある媒質を通る光で，光に垂直な平面を通る光は単位距離進むごとに光の量は１/ｂ倍となってゆく。

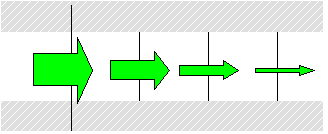
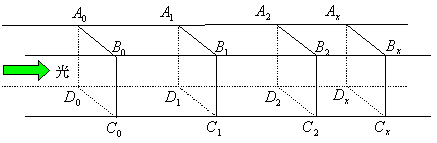
　図のように直方体でできている媒質があり光がこの中を通りぬけてゆくとする。この図には書いていないが，この媒質の周囲は一切光を通さない物質で固められていて，Ａ₀Ｂ₀Ｃ₀Ｄ₀面に垂直な光はこの直方体の中だけを通ってゆくことができるようになっている。光はこの内部を通りながらこの媒質に少しずつ吸収されてＡ₀Ｂ₀Ｃ₀Ｄ₀面を通る光の量は次第に減少し，Ａ₁Ｂ₁Ｃ₁Ｄ₁面を通るときはＡ₀Ｂ₀Ｃ₀Ｄ₀面を通るときの光の量の１/ｂになっている(１/ｂ＝ａとする）。

　今媒質内を１ｍ進むごとにａ倍になるとする。

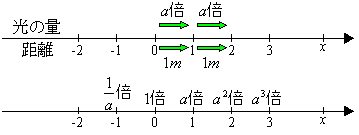
　光は１ｍ進むとａ倍になるのだから，２ｍ進むとａ倍の更にａ倍つまりａ²倍となり，３ｍ進むとａ³倍となる。以下同様に考えてゆけばよい。ところで光はＡ₀Ｂ₀Ｃ₀Ｄ₀面を通ってから１ｍ進んでＡ₁Ｂ₁Ｃ₁Ｄ₁面を通ることになるのだが，１ｍ進んだところで急にａ倍になるということではなく少しでも進んでゆけば前より光の量は減少し，進むたびごとに吸収されて１ｍ進んだ時点でａ倍になっていたということなのである。従ってＡ₀Ｂ₀Ｃ₀Ｄ₀面より１．５ｍ進んだ面を通る光の量はＡ₀Ｂ₀Ｃ₀Ｄ₀面を通り抜ける光の量の何倍かになっている筈である。ここで光が１ｍ進むとａ¹倍，２ｍ進むとａ²倍，３ｍ進むとａ³倍・・・となってゆくことから，１．５ｍ進んだ場合はａ^1.5倍になっていると考えることにするのである。このａ^1.5倍とは実際に何倍くらいになるのかということはあとでゆっくりと考えることにして，とにかく光が１．５ｍ進んだならばａ^1.5倍になるというように考えてゆこうということなのである。

(問)次のところでは０のところの光の量の何倍の光が通り抜けているか。

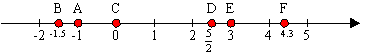
　今目盛がｘの位置を通る光の量をＩ_xと表わすことにすれば
　　　Ｉ₁＝ａＩ₀，　Ｉ₂＝ａＩ₁＝ａ²Ｉ₀，　Ｉ₃＝ａ³Ｉ₀，　・・・
であるが，ｘが整数でない場合でもＩ_5/2＝ａ^5/2Ｉ₀等というように表わすことができる。

　Ｏの位置から右にｘｍ進んだとき，Ａ_xＢ_xＣ_xＤ_xを通る光の量はＡ₀Ｂ₀Ｃ₀Ｄ₀を通る光のｙ倍になっていたとすれば，Ｉ_x＝ｙＩ₀でありＩ_x＝ａ^xＩ₀であるから，ｙ＝ａ^xである。（今後簡単に表現するために面Ａ₀Ｂ₀Ｃ₀Ｄ₀を通る光とか，面Ａ_xＢ_xＣ_xＤ_xを通る光というかわりに目盛Ｏを通る光，目盛ｘを通る光という表現を用いることにする。）

　この場合ｘが負の数であってもかまわない。目盛Ｏの位置から左に１ｍ離れた位置は−１の位置，左に２ｍ離れた位置は目盛−２の位置等と呼べばよく，
　　　Ｉ_-1＝ａ^-1Ｉ₀，　Ｉ_-2＝ａ^-2Ｉ₀，・・・，　Ｉ_-x＝ａ^-xＩ₀
となる。

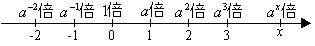
　特にＯの位置ではＯの位置より零ｍ進んだ位置と考えればよいからそこを通る光についてはＩ₀＝ａ⁰Ｉ₀であり，Ｉ₀＝Ｉ₀は自明であるから　ａ⁰＝１　となる。