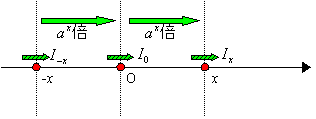
次にOの位置よりもxm前までは,そこを通る光の量はI0の何倍であった答えなのかを考えよう。
これはまずOの位置に対して-xの位置と考えられるからここでの光の量については I-x=a-xI0 が成り立つ。また-xの位置からxmだけ光が進むとOの位置に達するのであるから,I-xという量の光がxm進むことによりax倍となりそれがI0という光の量になっている。つまり I-x×ax=I0 となる。故に I0/ax=a-xI0 となり a-x=1/ax が導かれる。

このことについては別な考え方もできる。光は与えられた媒質の中を左から右の方向へ進んでいて,1m進むごとに光の量はa倍になっていくのであった。
従ってI-1はI0の1/a倍,I-2はI-1の1/a倍,・・・となっているから
I-2=(1/a)2I0, I-3=(1/a)3I0, ・・・
となり I-x=(1/a)xI0 が得られる。
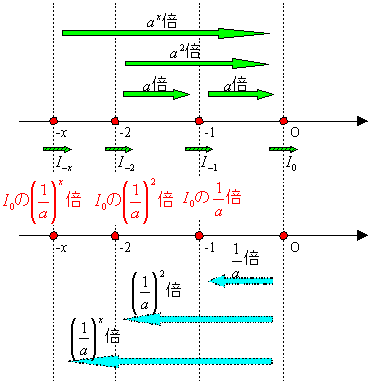
I-x=(1/a)xI0 と I-x=a-xI0 より (1/a)x=a-x
従って (1/a)x=a-x=1/ax が得られる。
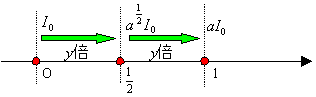
Oの位置より1/2m進むと光の量は何倍になっているのだろうか。それはI0のa1/2倍であるといえばよいのだが,実際には何倍のことだろうか。y=a1/2とおいて考える。光は1/2m進むごとにy倍となるのだから I1/2=yI0,また I1=yI1/2=y2I0 となりI1=aI0 より y2=a が得られる。故に y=√a つまり a1/2=√a である。
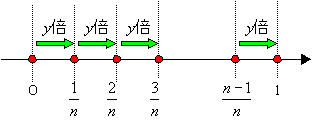
I1/n=a1/nI0のときy=a1/nとおいて,このyについて考えてみよう。これは1/n m進むごとにy倍となることを繰り返しているから光の量については次のような関係が成り立つ。
I1/n=yI0, I2/n=yI1/n=y2I0, ・・・ , I1=yI(n-1)/n=ynI0
ところが I1=aI0 より
yn=a ∴ y=n√a
故に a1/n=n√a が成り立つ。

Oからm(m)進んだmの位置での光の量は Im=amI0 となっているが,これをn段階に分割して考えてみることにする。m(m)進むのにm/n(m)ずつn回進むことによってm(m)進んだと考えるのである。
Im/n=am/nI0 であるが,y=am/n とおいてこのyについてかんがえてみることにする。m/n(m)進むごとにy倍となることを繰り返してゆくので光の量について次の関係が成り立つ。
Im/n=yI0, I2m/n=yIm/n=y2I0, ・・・ , Im=yI(n-1)m/n=ynI0
また Im=amI0 であるから yn=am が成り立つ。
故に y=n√am となるので am/n=n√am が成り立つ。
[1]次の式を根号の形でかけ。
| (1) a1/3 | (2) a2/5 | (3) a-1/4 | (4) a-2/5 | (5) b3/2 |
| (6) b-5/2 | (7) p-1/3 | (8) t-2/3 | (9) t2 3/4 | (10) t-1 2/5 |
[2]次の式をaxの形でかけ。
| (1) √a3 | (2) 3√a2 | (3) 1/a3 | (4) 1/a5 | (5) 1/√a |
| (6) 1/3√a4 | (7) 3√a5 | (8) 4√a-3 | (9) 1/(3√a)2 | (10) 6√a3 |
| (11) 4√a3 | (12) 5√a6 | (13) 1/√a3 | (14) 3√a-6 | (15) 1/(3√a5)6 |
[3]次の等式の左辺をamの形に直し,( )に適当な数を記入せよ。
| (1) √5=5( ) | (2) 1/53=5( ) | (3) 1/81=3( ) |
| (4) 3√81=3( ) | (5) 0.001=10( ) | (6) 4√125=5( ) |
| (7) 4√625=5( ) | (8) 5√43=2( ) | (9) 1/5√43=2( ) |
今まで調べてきたことをまとめてみよう。I2=a2I0 であったがa2とはa倍の繰り返しであった。nが正の整数のときにはanはa倍をn回続けるという意味になる。ところがa5/2等はa倍を2.5回繰り返す等と考えても意味がない。これは5/2の位置を通る光の量I5/2が,Oの位置を通る光の量I0のa2.5倍であると意味であり,それは a5/2=√a5 であるということは既に調べてきたのであった。また a-3/5 等はどんな意味を持つかということについても調べてきた。それは-3/5の位置を通る光の量I-3/5がOの位置を通る光の量I0のa-3/5倍になることを示す数であり a-3/5=1/a3/5=1/5√a3 となることであった。
このようにanという場合のnとは正の整数だけでなく,正負の有理数であってもよいのである。