丂倎m偼侾偵倎傪倣屄妡偗傞丆倎n偼侾傪値夞妡偗傞偙偲偱偁傞偐傜丆
丂丂丂
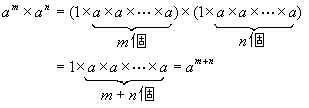
偲側傞丅
丂偝偰崅峑悢妛偺幃寁嶼偱傛偔梡偄傜傟偐偮廳梫側栶妱傪偼偨偡傕偺偼丆寁嶼偺婎杮朄懃偲偟偰偺岎姺懃丆寢崌懃丆暘攝懃偲嫟偵巜悢朄懃偲偄傢傟傞傕偺偱偁傞丅巜悢朄懃偲偼師偺傛偆側岞幃傪偄偆丅
|
倣丆値偑惓偺惍悢偺偲偒 丂丂丂丂丂倎m亊倎n亖倎m+n丆 丂丂丂丂丂倎m亐倎n亖倎m-n 丂丂丂丂丂(倎m)n亖amn丆 丂丂丂丂丂(倎倐)m亖倎m倐m 偲側傞丅 |
丂偙傟傜偺岞幃偺徹柧偼丆椺偊偽師偺傛偆偵偟偰側傢傟傞偙偲偑懡偄丅
丂倎m偼侾偵倎傪倣屄妡偗傞丆倎n偼侾傪値夞妡偗傞偙偲偱偁傞偐傜丆
丂丂丂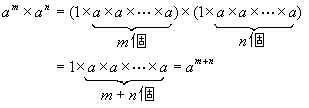
偲側傞丅
丂偟偐偟側偑傜倣傗値偑惓傗晧偺桳棟悢偱偁傟偽丆偙偺傛偆側曽朄偱偺徹柧偼偱偒側偄丅廬偭偰倣丆値偑桳棟悢偺偲偒偵巜悢朄懃偑惉傝棫偮偐偳偆偐傕敾傜側偄傢偗偱偁傞丅偨偲偊偽丆
丂丂丂倎-5亊倎3亖倎-5+3亖倎-2
丂丂丂倎2/5亊倎1/3亖倎2/5+1/3亖倎11/15
丂丂丂(倎-2/3)4/5亖倎-2/3亊4/5亖倎-8/15
摍偲偄偆傛偆偵寁嶼偟偰傕傛偄偺偱偁傠偆偐丅
丂偙傟傪峫偊傞応崌偵傕攠幙偺拞傪捠傞岝偺検偵偮偄偰偺惈幙傪傕偲偵偟偰寁嶼朄懃傪尒偮偗偰備偐側偗傟偽側傜側偄丅
丂岝偼俷偺埵抲傛傝栚惙倶1偺埵抲偵摓払偟丆偦偙偐傜嫍棧倶2偩偗恑傫偱栚惙倶1亄倶2偺埵抲偵払偡傞丅偙偺応崌偵偮偄偰峫偊傛偆丅
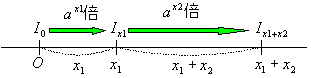
丂俬x1亖倎x1俬0丆俬x1+x2亖倎x2俬1傛傝
丂丂丂俬x1+x2亖倎x2亊倎x1俬0
丂丂丂俬x1+x2亖倎x1+x2俬0
屘偵
丂丂丂倎x1+亊倎x2亖倎x1+x2
偑惉傝棫偮丅偟偐傕偙偺応崌偺倶1丆倶2偼惓丆晧偺桳棟悢偱偁偭偰傕忋幃偼惉傝棫偮丅
丂師偵俬x1亖倐俬0偲偡傞丅偙偺偲偒俬x1亖倎x1俬0偱偁傞偐傜丆倐亖倎x1偱偁傞丅侽偐傜倶1傑偱傪扨埵嫍棧偲傒側偟偨偲偒丆侽偐傜栚惙倶1倶2傑偱偺嫍棧偼偙偺扨埵嫍棧偺倶2攞偲側偭偰偄傞丅偙傟偼俷傪捠傞岝偑扨埵嫍棧恑傓偛偲偵倐攞偵側偭偰備偔偲偒丆偦偺扨埵嫍棧偺倶2攞偺嫍棧傪恑傫偩偲峫偊傜傟傞丅
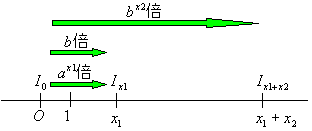
丂栚惙倶1倶2傪捠傞岝偺検偼俬x1x2亖倐x2I0偲側傞丅傑偨俬x1x2亖倎x1x2I0偱偁傞偐傜倐x2亖倎x1x2偲側傞丅倐亖倎x1傛傝
丂丂丂(倎x1)x2亖倎x1x2
偑惉傝棫偮丅
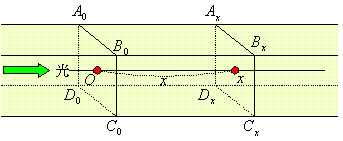
丂忋恾偺傛偆側攠幙偺拞傪岝偑捠傝偸偗偰備偔丅偙偺攠幙傪捠傞岝偺検偼侾倣恑傓偛偲偵倎倐攞偲側偭偰備偔偲偡傞丅
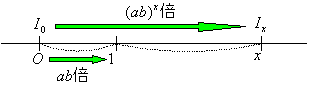
丂廬偭偰俬x亖(倎倐)xI0偲側傞丅岝偺検偵偮偄偰峫偊傞偲丆偼偠傔I0偱偁偭偨傕偺偑丆偙偺攠幙偺拞傪倶倣恑傫偱Ix偵側偭偨偺偱偁傞偑丆偙偺Ix偵偮偄偰偼師偺偙偲偑偄偊傞丅
丂傑偢丆I0偑侾倣恑傓偲倎倐攞偵側傞攠幙偺拞傪捠傝俬1偲側傞偑俬1亖倎倐俬0偱偁偭偨丅偙偺俬1偵偮偄偰偼師偺傛偆偵抜奒偵暘偗偰峫偊傞偙偲偑偱偒傞丅
丂傑偢俬0偑侾倣恑傓偛偲偵倎攞偲側傞攠幙偺拞傪侾倣恑傒俬1乫偲側傝丆堷偒懕偄偰俬1乫偑侾倣恑傓偛偲偵倐攞偲側傞攠幙偺拞傪侾倣恑傫偱俬1''偲側傞偲偒丆俬1''亖俬1偱偁傞丅壗屘側傜偽丂俬1乫亖倎俬0丆俬1''亖倐俬1乫亖倐倎俬0丂偱偁傝丆俬1''亖俬1丂偑偄偊傞丅偮傑傝俬0偑侾倣恑傓偲倎倐攞偲側傞攠幙偺拞傪侾倣恑傓偲偄偆偙偲偼丆侾倣恑傓偲倎攞偲側傞攠幙偺拞傪侾倣恑傒丆堷偒懕偄偰侾倣恑傓偲倐攞偲側傞攠幙偺拞傪侾倣恑傓偲偄偆偙偲偲摨偠岝偺検偵側傞偺偱偁傞丅
丂偙偺峫偊傪偮偒偮傔偰備偔偲俬0偑侾倣恑傓偛偲偵倎倐攞偲側傞攠幙偺拞傪倶倣恑傫偩偲偒偺岝偺検偼丆俬0偑傑偢侾倣恑傓偛偲偵倎攞偲側傞攠幙偺拞傪倶倣恑傒丆堷偒懕偄偰侾倣恑傓偛偲偵倐攞偲側傞攠幙偺拞傪倶倣恑傫偩偲偒偺岝偺検偲摨偠偵側傞偺偱偁傞丅
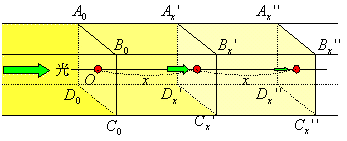
丂俬0偑侾倣恑傓偲倎倐攞偲側傞攠幙偺拞傪倶倣恑傫偩偲偒偺岝偺検偼丆俬x亖(倎倐)x俬0偱偁傞丅傑偨俬0偑侾倣恑傓偲倎攞偲側傞攠幙拞傪倶倣恑傒岝偺検偼俬x乫偲側傝丆堷偒懕偄偰侾倣恑傓偲倐攞偲側傞攠幙拞傪倶倣恑傫偱岝偺検偼俬x''偲側偭偨偲偟傛偆丅偙偺偲偒師偺幃偑惉傝棫偮丅
丂丂丂俬x乫亖(倎x)俬0丆丂丂俬x''亖倐x俬x乫亖倎x倐x俬0
丂婛偵峫嶡偟偰偒偨傛偆偵俬x亖俬x''偱偁傞偐傜丆(倎倐)x亖倎x倐x俬0偲側傝丆屘偵
丂丂丂(倎倐)x亖倎x倐x
偑惉傝棫偮丅