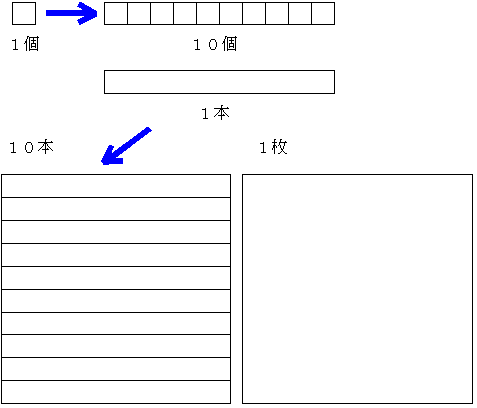
壱を10集めると拾となり、拾を10集めると百となり、百を10集めると千となる・・・。そして数を表すには、例えば百が2つに、拾が5つ、壱が4つを2×(百)＋5×(拾)＋4×(壱)と書き254と表す。これは数を表すのに、基本となる単位を設定し、それらの単位がそれぞれ何個ずつ集まっているかを、位取りを明示しつつ表していることの具体的な例である。そしてある位の単位が10集まる毎に次の位の単位を構成していくことを示しており、このことから10進数とか10進法による記数法と呼ばれる。これを図の上で明確に示すこともできる。今、長さを定めた或る正方形の図で「1」を表すことにしよう。

　この正方形が10個集まって一本の細長い棒状の長方形となるが、この図一本が「10」を表すことになる。

　更にこの長方形が10本集まって大きな正方形となり、この正方形1枚が「10²」を表すことになる・・・。このように正方形が10個集まる毎に棒状の正方形が1本形成され、この長方形が10本集まって大きな正方形が1枚形成される。更にこの大きな正方形が10枚集まってより巨大な棒状の正方形が形成され、その巨大な長方形が10本集まってもっと巨大な正方形が着せ征される・・・。このようにして「1」から「10」、「10」から「10²」、「10²」から「10³」・・・へと正方形、長方形、正方形、長方形、と図が巨大な図となってゆき、位取りが進んでいく様子を視覚化させることができる。

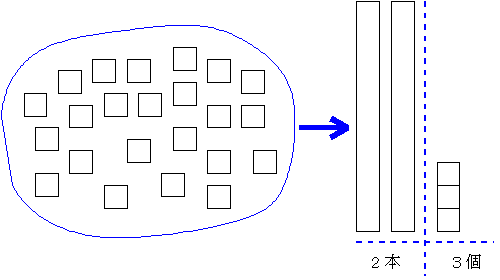
　ここで次のような正方形の図が散乱した状態の表している数について考えてみよう。

　まとめてみると2本と3個であるから「23」を表しているが、2本を表す2と3個を表す3とを書き表すことにより、その意味が的確に伝えられる。つまり「23」の2と3は「10」の係数の2と「1」の係数の3とを並べて書いていることにより2×10＋3×1の意味を表しているといってよい。

　では1より小さい数は正方形の図を用いてどのように表せるのであろうか。

　先ほど考えた「1」を表す正方形の図、□を細分化してゆくことを考えるとよい。つまり□の図は、この図を10等分して細分化された細長い長方形の図が10本集まってできた正方形であると考えるのである。これを図の上で考えると余りにも小さな図となってしまうので独特な虫めがねで任意に拡大された図をもとにして調べてゆくことにしよう。

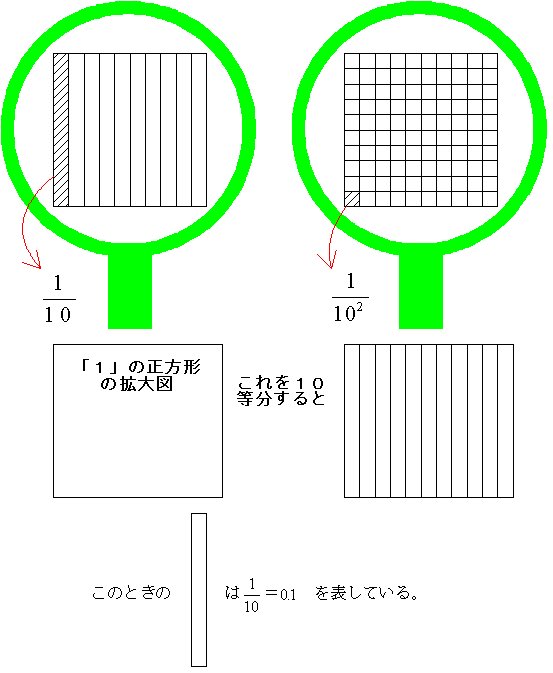
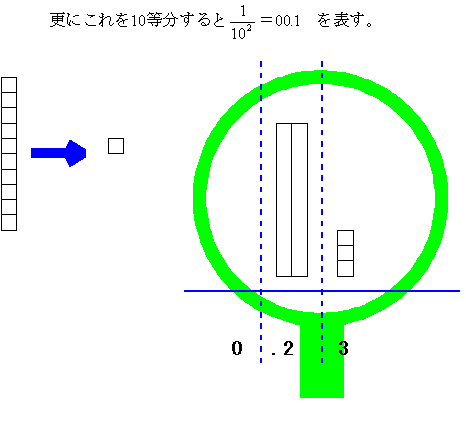
　図のように細分化された長方形が2本と、その長方形を更に10等分した正方形が3個で表される数は2×1/10+3×10²を表し、これを0.23と表している。