乲栤俆乴慜偺乮栤係乯偺寢壥偲丆僆僀儔乕偺懡柺懱掕棟偲傪梡偄偰丆師偺偙偲傪徹柧偣傛丅乬惓懡柺懱偼俆庬椶傛傝懡偔側偄丅惓巐柺懱丆惓榋柺懱丆惓敧柺懱丆惓廫擇柺懱丆惓擇廫柺懱偵尷傞乭 |
乮徹柧乯惓懡柺懱偵偍偄偰捀揰偺悢傪倕丆柺偺悢傪倖丆慄偺悢傪倠偲偡傞偲僆僀儔乕偺懡柺懱掕棟傛傝
丂丂丂倕亄倖亅倠亖俀丒丒丒嘆
偱偁傞丅
丂惓懡柺懱側偺偱奺柺偺慄偺悢傪偡傋偰値丆侾偮偺捀揰偵廤傑傞慄傪偡傋偰倣偲偍偔偙偲偑偱偒傞丅
丂乲栤係乴偺寢壥傛傝丂倣倕亖俀倠丒丒丒嘇丆値倖亖俀倠丒丒丒嘊偑惉傝棫偮丅
丂屘偵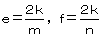 傪嘆偵戙擖偡傞偲
傪嘆偵戙擖偡傞偲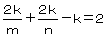 偲側傝
偲側傝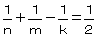 偲側傞丅
偲側傞丅
丂偙偙偱懡柺懱偑偱偒傞偨傔偵偼丂倠亞侾丆倣亞俁偱倠丆倣丆値偼惍悢偱偁傞丅
丂乲栤侾乴偺寢壥傛傝忦審傪枮偨偡夝偼師偺俆捠傝偱偁傞丅
(1)値亖俁丆倣亖俁丆倠亖俇
丂丂丂屘偵丂倖亖係偱惓巐柺懱乮奺柺偼嶰妏宍乯
(2)値亖俁丆倣亖係丆倠亖侾俀
丂丂丂屘偵丂倖亖俉偱惓敧柺懱乮奺柺偼嶰妏宍乯
(1)値亖俁丆倣亖俆丆倠亖俁侽
丂丂丂屘偵丂倖亖俀侽偱惓擇廫柺懱乮奺柺偼嶰妏宍乯
(1)値亖係丆倣亖俁丆倠亖侾俀
丂丂丂屘偵丂倖亖俇偱惓榋柺懱乮奺柺偼巐妏宍乯
(1)値亖俆丆倣亖俁丆倠亖俁侽
丂丂丂屘偵丂倖亖侾俀偱惓拞偵柺懱乮奺柺偼屲妏宍乯
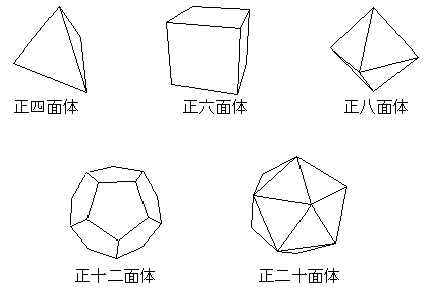
丂埲忋偺寢壥傛傝惓懡柺懱偼俆庬椶偩偗偱偁傝丆偟偐傕偦傟傜偺侾偮侾偮偺柺偑偳偺傛偆側懡妏宍偱偱偒偰偄傞偐偑敾傞偺偱偁傞丅
丂丂丂丂乻丂嶲丂峫丂帒丂椏丂乼