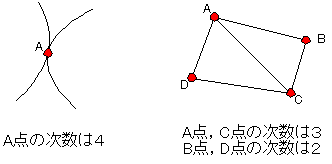
〔問４〕次を証明せよ。 (1)リニア・グラフの各点の次数の総和は線の数の２倍になる。 (2)単純多面体において，各面をかこむ線がすべてｎ本，１つの頂点に集まる線の数がすべてｍ本とするとき 　　ｍｅ＝２ｋ，ｎｆ＝２ｋ となる。

(証明)
(1)リニア･グラフにおいて線は必ず２つの点を結んでいるので，各点の次数を算あげるとき，それぞれの線はその両端の点で１回づつ（つまり１本の線が２度づつ）算えられている。

(2)図でＡとＢをつなぐ線は点Ａに集まる線として，また点Ｂに集まる線として，算えられている。ｅ個の点に集まる線を算えるとき１本の線が２度づつ算えられることになる。（(1)より）故に　ｍｅ＝２ｋ

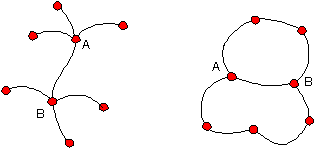
　次に１つの面をとりまく線の数がすべてｎで面の数がｆとすると，すべての面をとりまく線の数はｎｆとなるが，これは図の線ＡＢのように面αをとりまく線としても，面Ｂをとりまく線としても算えあげられていて，ｋ本の線のすべてが二度ずつ算えあげられている。その合計がｎｆであるからｋの２倍とｎｆとは等しい。故に　ｎｆ＝２ｋ