単純多面体において一つの面だけを取り除いたものを考える。

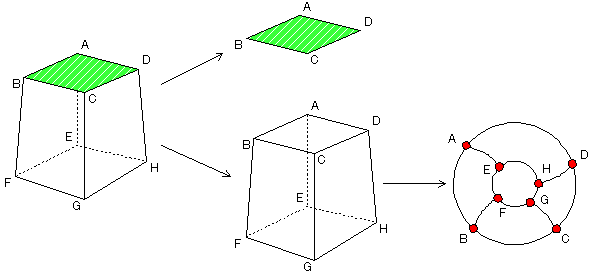
　一つの面を取り去った残りの立体は，位相変換によって単純閉曲線を連結させた図形にすることができる。

　いよいよ単純閉曲面において点の数，面の数，線の数の関係について考えることにしよう。
　これがオイラーの多面体定理と呼ばれるものである。

〔問３〕任意の凸多面体において，頂点の数，面の数，線の数をそれぞれｅ，ｆ，ｋとすると 　　　ｅ＋ｆ−ｋ＝２ となることを証明せよ。

（証明）凸多面体から一つの面だけを取り去ったものを考える。これを位相変換させると，単純閉曲線を連結させた図形になる。この図形においては
　　　ｅ＋ｆ−ｋ＝１
が成り立つ。次に取り去った面をもとの多面体に再び取り付けて復元する。このとき点の数，線の数に変化はなく，面の数だけが１つ増える。
　故に凸多面体においては
　　　ｅ＋ｆ−ｋ＝２
が成り立つ。