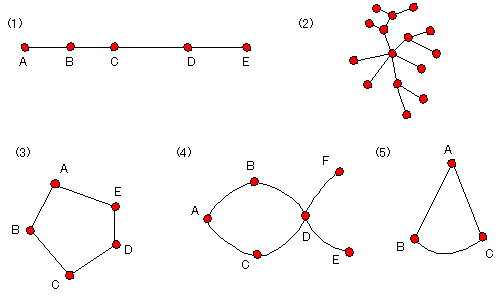
丂慜偵彂偄偨恾偱(1)偲(3)丆(5)偲偼堘偆惈幙傪帩偭偰偄傞丅
丂(1)偼堦捈慄偲摨憡側恾偱偁傝丆(3)丆(5)偼墌偲摨憡側恾宍偱偁傞丅偙偺傛偆偵墌偲摨憡側恾宍傪扨弮暵嬋慄偲偄偆丅
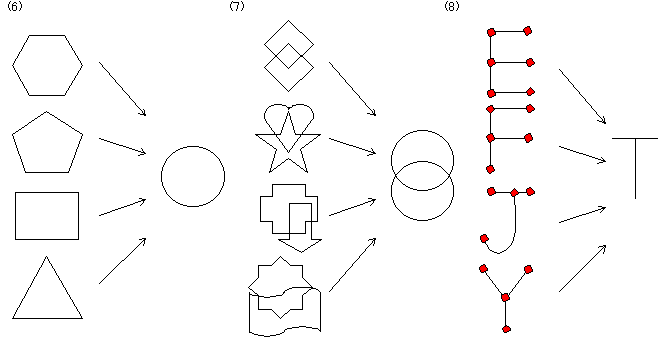
丂扨弮暵嬋慄偼昁偢暯柺傪撪晹偲奜晹偺擇偮偺椞堟偵暘偗傞丅忋偺(6)恾偼偄偢傟傕扨弮暵嬋慄偱偁傝丆(7)偺恾偼扨弮暵嬋慄偑楢寢偟偨傕偺偱偁傝丆(8)偺恾偼扨弮暵嬋慄偱偼側偄丅
丂偦偙偱扨弮暵嬋慄偱偺撪晹偺椞堟偺偙偲傪崱屻乵柺乶偲屇傇偙偲偵偡傞丅偱偼偄偔偮偐偺恾宍偵偍偄偰丆揰丆慄丆柺偺悢偺娫偵偳傫側娭學偑偁傞偐挷傋偰傒傛偆丅偙偙偱偼(7)偺傛偆側扨弮暵嬋慄傪楢寢偝偣偨恾宍傪拞怱偵偟偰峫嶡偟偰傒傞偙偲偵偟偨偄丅揰偺悢傪e丆柺偺悢傪倖丆慄偺悢傪倠偲偡傞丅
丂(9)恾偱偼丂倕亄倖亅倠亖係亄俀亅俆亖侾丂偲側傞丅
丂(10)恾偱偼丂倕亄倖亅倠亖係亄俀亅俇亖侾丂偲側傞丅
丂(11)恾偱偼丂倕亄倖亅倠亖俆亄俀亅俇亖侾丂偲側傞丅
丂(12)恾偱偼丂倕亄倖亅倠亖俋亄俁亅侾侾亖侾丂偲側傞丅
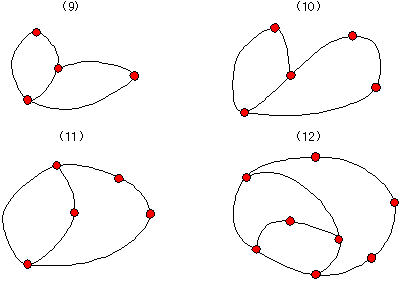
丂偙偺傛偆偵峫偊傞偲堦斒偵
丂丂丂倕亄倖亅倠亖侾
偲側傞偙偲偑梊憐偝傟傞丅偙偺偙偲傪師偺弴偱徹柧偟傛偆丅
乲栤俀乴扨弮暵嬋慄傪楢寢偝偣偨恾宍偵偮偄偰
丂丂丂乮揰偺悢乯亄乮柺偺悢乯亅乮慄偺悢乯亖侾
丂偲側傞偙偲傪師偺弴偱徹柧偣傛丅
(1)丂扨弮暵嬋慄傪娷傑側偄儕僯傾O儔僼乮暵偠偨恾宍乯偱偼
丂丂丂丂乮揰偺悢乯亅乮慄偺悢乯亖侾偑惉傝棫偮丅
(2)丂扨弮暵嬋慄偱偼
丂丂丂丂乮揰偺悢乯亄乮柺偺悢乯亅乮慄偺悢乯亖侾偑惉傝棫偮丅
(3)丂扨弮暵嬋慄傪楢寢偝偣偨恾宍偱偼
丂丂丂丂乮揰偺悢乯亄乮柺偺悢乯亅乮慄偺悢乯亖侾偑惉傝棫偮丅
|
乮夝乯
(1)慄偺悢偑侾偺偲偒偼揰偺悢偼俀偱偁傞偐傜乮揰偺悢乯亅乮慄偺悢乯亖侾偼惉傝棫偮丅師偵慄偺悢偑倠偺偲偒偵傕忋幃偑惉傝棫偮偲壖掕偡傞丅
丂慄偺悢傪倠亄侾偵偡傞偲偒丆怴偨側侾杮偺抂揰傪崱傑偱偺恾偺揰偺偳偙偐偵慖傇偲偒偼丆憹偊傞揰偼侾屄偲憹偊傞慄傕侾杮偱偁傞丅
丂屘偵乮揰偺悢乯亅乮慄偺悢乯亖侾偑惉傝棫偮丅
丂傑偨怴偟偔壛偊傞侾杮偺慄偺抂揰傪崱傑偱偺恾偺慄偺搑拞偵嶌傞偲偒偼憹偊傞揰偼俀屄偱丆憹偊傞慄傕俀杮偵側傞丅屘偵偙偺偲偒傕乮揰偺悢乯亅乮慄偺悢乯亖侾偑惉傝棫偮丅埲忋偱悢妛揑婣擺朄偵傛傞徹柧傪廔傢傞丅

(2)扨弮暵嬋慄偱偼乮揰偺悢乯偲乮慄偺悢乯偼摍偟偔側傞丅偙傟傕悢妛揑婣擺朄偱徹柧偱偒傛偆丅
丂傑偨柺偺悢偼侾偱偁傞丅廬偭偰乮揰偺悢乯亄乮柺偺悢乯亅乮慄偺悢乯亖侾偲側傞丅

(3)扨弮暵嬋慄傪楢寢偝偣傞偲偒侾偮偺扨弮暵嬋慄偲懠偺扨弮暵嬋慄偲偺嫬奅偼奐偄偨恾宍偱偁傞丅廬偭偰嫬奅傪側偟偰偄傞奐偄偨恾宍偺揰偺悢傪兛丆慄偺悢傪兝偲偡傞偲丆
丂丂兛亅兝亖侾丒丒丒嘆丂偱偁傞丅
丂傑偨侾偮偺扨弮暵嬋慄偺揰偺悢丆慄偺悢傪偦傟偧傟倕侾丆倠侾丆偙傟偲楢寢偟偰偄傞懠偺扨弮暵嬋慄偺揰偺悢丆慄偺悢傪倕俀丆倠俀偲偡傞偲師偑惉傝棫偮丅
丂丂倕侾亄侾亅倠侾亖侾丒丒丒嘇
丂丂倕俀亄侾亅倠俀亖侾丒丒丒嘊
丂俀偮偺扨弮暵嬋慄傪楢寢偝偣偨恾宍偵偍偄偰偼揰偺悢丆柺偺悢丆慄偺悢偼偳偆側傞偱偁傠偆偐丅
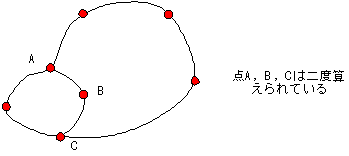
丂倕侾亄倕俀偺拞偵偼丆嫬奅偺奐偄偨恾宍偺揰傪俀搙嶼偊偨傕偺偑娷傑傟偰偄傞丅
丂廬偭偰楢寢恾宍偺揰偺悢偼倕侾亄倕俀亅兛偱偁傞丅摨條偵偟偰楢寢恾宍偺慄偺悢偼倠侾亄倠俀亅俛偱偁傞丅偦偙偱楢寢恾宍偺
丂丂乮揰偺悢乯亄乮柺偺悢乯亅乮慄偺悢乯亖侾
偼師偺傛偆偵側傞丅
丂丂乮倕侾亄倕俀亅兛乯亄乮侾亄侾乯亅乮倠侾亄倠俀亅俛乯
丂丂亖乮倕侾亄侾亅倠侾乯亄乮倕俀亄侾亅倠俀乯亅兛亄俛
丂丂亖侾亄侾亅侾亖侾