�g���C���C���͎��R���ŁC�����������Ƃ���B�������C���C���̒l��S�ċ��߂�B�h
�@�܂��C���̖��������Ă݂悤�B
�@�������������C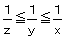 �ł���B
�ł���B
�@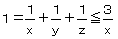 �@�@�@�̂�
�@�@�@�̂�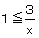 ���
���
�@�@�����R�C�@�����P���@�Q�������R
(1)�����Q�̂Ƃ�
�@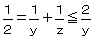 ���@�����S
���@�����S
�@�����Q������@�R�������S
�@(i)�����Q�C�����R�̂Ƃ��@�����U
�@�@�@�̂Ɂ@�����Q�C�����R�C�����U
�@(ii)�����Q�C�����S�̂Ƃ��@�����S
(2)�����R�̂Ƃ�
�@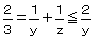 ���@�����R
���@�����R
�@�����R�C�����R�̂Ƃ��@�����R
�@�ȏ�̉�@�𗝉�����Ȃ�C���̖�ɉ��邱�Ƃ͔�r�I�ȒP�ɂł���ł��傤�B
|
�k��P�l���C���C�������ꂼ�ꂍ���R�C�����R�C�����P�̐����Ƃ��āC���̎��������C���C���̒l�����ׂċ��߂�B �@�@�@ 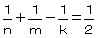
|
�i���j�����P�C�����R���
�@�@�@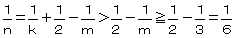 �@�@�@���@
�@�@�@���@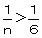 �C��<�U�@�@�̂Ɂ@�����T
�C��<�U�@�@�̂Ɂ@�����T
�@�܂��C�����R���@�@�R�������T�@�@�]���ā@�R=�R�C�S�C�T�ɂ��Ē��ׂ�B
(�T)�����R�̂Ƃ�
�@�@�@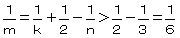 �@�@�@���@�R�������T
�@�@�@���@�R�������T
�@(�)�����R�C�����R�̂Ƃ�
�@�@�@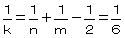 �@�@�@�������U�@�@���@�����R�C�����R�C�����U
�@�@�@�������U�@�@���@�����R�C�����R�C�����U
�@(�)�����R�C�����S�̂Ƃ�
�@�@�@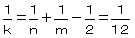 �@�@�@�������P�Q�@�@���@�����R�C�����R�C�����P�Q
�@�@�@�������P�Q�@�@���@�����R�C�����R�C�����P�Q
�@(�)�����R�C�����T�̂Ƃ�
�@�@�@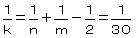 �@�@�@�������R�O�@�@���@�����R�C�����T�C�����R�O
�@�@�@�������R�O�@�@���@�����R�C�����T�C�����R�O
(�U)�����S�̂Ƃ�
�@�@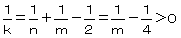 ���@�R�������S
���@�R�������S
�@�@�����(�T)��(�)�ɂ����āC���Ƃ�����ꂩ�������̂ɂȂ邩��@�����S�C�����R�C�����P�Q
(�V)�����T�̂Ƃ�
�@�@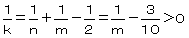 �@���@
�@���@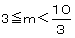
�@�����R�̏ꍇ�݂̂ɂ��Ē��ׂ��
�@�@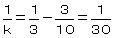 �@�@�@���@�����R�O�@�@�̂Ɂ@�����T�C�����R�C�����R�O
�@�@�@���@�����R�O�@�@�̂Ɂ@�����T�C�����R�C�����R�O
�@���������̖��������������ł́C���̂��Ƃłǂ�ȈӖ��������Ă���̂��Ȃǂ͂܂�����Ȃ��B�v����ɂ��C���C���̑g�͂T�g�����Ȃ��Ƃ������Ƃ��͂����藝������邾���ŏ[���ł���B