同じｘ＝２^ｘを　底の異なるｌｏｇ_２　のめがねとｌｏｇ_ａのめがねで見た対数表をつくると

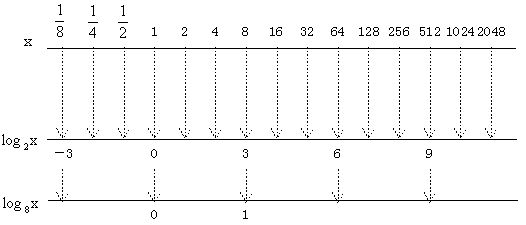
　これを見ると底の異なるｌｏｇのめがねで見た対数表どうしは
　　（底が大きくなれば値が小さくというように）互いに比例している。

　この関係をつかえばｌｏｇ_８ｘのあいている値も簡単にもとめられる。

　底を８から２に変える場合、ｌｏｇ_８ｘの値はｌｏｇ_２ｘの値に１／３かければ良い。この３という値はｌｏｇ_２のめがねで見た値。

　つまり、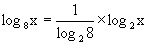　という関係になっている。

　一般に底をａからｂに変えるためには
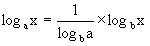　　　　　とすればよい。

　つまり、　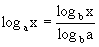　　　 　これを底の変換公式という。

　この関係をつかえば、ひとつくわしい対数表があればすべての対数を求めることができる。

例　ｌｏｇ_８２５６＝―――――＝

練習　底の変換公式を用いて、次の対数の値を求めよ。

　�@　ｌｏｇ _８ １０２４

　�A　ｌｏｇ _４ ８

　�B　ｌｏｇ _１６ １２８

　�C　ｌｏｇ _９ ２４３

　世の中ではこのひとつくわしい対数の表として、１０を底とするｌｏｇ_１０ｘの対数表をよく用いる。この１０を底とする対数を常用対数という。
　教科書の後ろに小数点以下４ケタの常用対数表がのっている。