

0.はじめに
指数関数や対数関数の分野は、自然や社会の現象との関係も深く、興味深い話題も多い。
このレポートは「対数は<自然>の倍の法則を<人間>の比例の法則にうつす眼鏡の役割をはたす」(森毅『数の現象学』朝日新聞社)という視点を基本に、対数の指導の展開を試みた授業の報告である。
対数関数は x=catという指数変化を、
log x=(log a)・t+log c
という1次関数に移す。そして、この対数関数の持つもっとも基本的な性質が、人間にとって認識しにくく予想もしにくい指数変化を、人間にとって自然な比例の世界へ移し、そこに線形性をあてはめることを可能にする。
この指数変化と比例的変化の対応のシェーマとして有効性を発揮するものが真数−対数の対応表である。乗法と加法を対応させる簡単な操作によって、対数関数の基本的な性質を導くことができる。
さらにこのような視点から底の変換公式を考えれば、その意味するところはある指数変化xの対応表どうしが
log b x=A log a x
という形で比例しているということにある。そして、この比例定数Aが、もとの底の対数で変換する底を見た値の逆数に、なっている。
こうした対数の指数変化のメガネとしての有効性を明示的に示すのが片対数グラフである。対数概念の理解にとってもまた実用的な有効性からも、最初の対数の指導の内容に片対数グラフの指導が含まれる必要がある。
以上のことから対数の指導プランの骨子を次のように設定した。
1.指数現象と対数 【プリントはここをクリック】
指数現象が人間にとって予想しにくいということを印象づけるための問題である。紙新聞を持っていって説明する。生徒の予想はイウエが多いが、カの生徒も各クラスに数人いる。解答は210=103を用いて次のようになる。
紙の厚さを0.1mmをすると
0.1mm×2100「百億光年だからほとんど宇宙のはて、ただし新聞紙の1辺の方も原子の直径よりずっと小さくなる」。生徒は驚いてくれる。
=0.1mm×1030 (2100=(103)10103)
=1029mm (mにすると)
=1026m (kmにすると)
=1023km (1光年=1023km)
=1010光年
=10000000000光年
2.対数表 【プリントはここをクリック】
この真数−対数の対応表の扱いがこの後の展開の基盤となる。積が和に対応していること及びそのことによって計算がきわめて簡単になることを、生徒にあ
る種の驚きをもって理解させたい。今回は「先生すごいね。誰が考えた?」などという反応などもあり、楽しく進められた。
公式にする部分は少し苦しい。3pでやったことの一般化であるということで、具体的な例を示しながら簡単に扱う。
この後、教科書の問題を使ってlogの計算練習を行った。
3.底の変換 【プリントはここをクリック】
同一の指数現象に対して底の異なる2つの対数表を対応させることによって、対数表どうしが比例していることが、簡単に確かめられる。このことが底の変換公式の自然な意味づけとなる。
このように logax と logbx が
log b x=A log a x
という形で比例しており、このときの比例定数Aが log b x の値になるのであるから、底の変換公式は
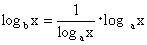
と表すのがもっともよくその本質的な関係を表現している。
さらに底の変換によって自由に底が選択できることを前提として、実用上便利な底として10が選ばれる。また自然対数としの低eもこうした認識のうえにたってはじめて(他の関数や微積分との諸関連の中で)自然な底として導入されるのではないだろうか。
授業ではこの後常用対数の計算練習と底の変換を用いる応用問題を扱った。
4.片対数グラフ 【プリントはここをクリック】
作業2はyの値の対数Yを同一のグラフ上にプロットするということで、生徒が混乱しやすい。yのグラフ上の点に値を書き込み、その値を対数メガネ log 10 で見た値をとるように指示する。作業3は2xの値を log 2 で見るということでxの値と等しくなるのは当然なのだが、指数現象のメガネとしての対数は本質的にその底に拠らない(底を変えても直線の傾きが変わるだけ)ということを印象づけるためには底の異なる対数でグラフをつくって見る必要があると考えた。
作業5のような片対数グラフの作成問題としては、世界の人口などのまっすぐなグラフになる例よりは、この例のような途中で大きく変化しているもののほうがグラフ作成の面白さがある。片対数グラフの例として日本の自動車の生産台数のデータを使うことについては、板倉聖宣・井藤伸比古『対数グラフの世界』(仮説社)を参考にした。データは『日本国勢図会』(国勢社)の巻末の長期統計のもので千の位で四捨五入してある。