2定点までの距離の比(商)が一定である点の軌跡
という定義を少し広げて
2定円までの接線の長さの比(商)が一定である点の軌跡
とすることを試みた。
そこで今度は
楕円 :2定点までの距離の和が一定である点の軌跡
双曲線:2定点までの距離の差が一定である点の軌跡
について同じことをするとどうなるか、調べてみた。
たとえば
2定円までの接線の長さの和が一定である点の軌跡
はどうなるか。
試みに具体例をひとつ。
2つの円
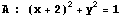
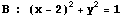
に対して、これら2円までの接線の長さの和が 2.1 である点の軌跡
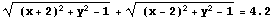
を考える。
「数学C」の教科書にあるように、この式から2度の両辺二乗を経て根号を解消し
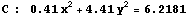
を得る。これは楕円の方程式であるが、グラフは次の図のようになる。
(赤色で表示。青色はもとの2円 A,B)
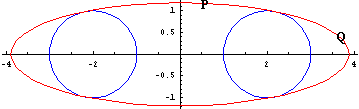
ここで、C上の点Pから2円にひいた接線の長さの和とQから2円にひいた接線の長さの和は明らかに異なるように見える。
そこで