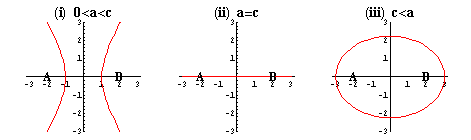楕 円:2定点までの距離の和が一定である点の軌跡
双曲線:2定点までの距離の差が一定である点の軌跡
の場合を考える。
(1)2定点からの距離の和が一定である点の軌跡
2定点 A(-c,0),B(c,0) までの距離の和が 2a(一定)である点 P(x,y)の軌跡を考える。ただし、a>c>0 とする。
点P(x,y) のみたすべき方程式は
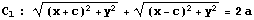
である。
このあと、「数学C」の教科書にあるように根号を解消するために両辺を2乗するという操作を経て次の式を得る。
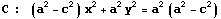
これは、a>c >0 により
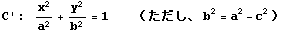
と変形され、これが楕円の方程式とされている。
まずa>c>0のとき、C1とC'が同じ図形を表すことを確認したい。
無条件に式として考えた場合
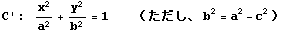
は次の4つの式の和集合("または")と同値である。
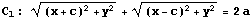
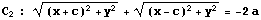
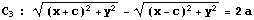
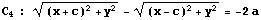
(∵)
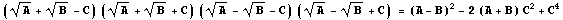
である。ここで
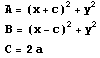
とおけば、右辺は
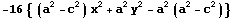
となり、できあがり。

またa>c>0より、C3は

つまり

よってこれをみたす点Pは存在しないからC3も表す図形なしである。
C4についても
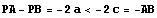
つまり

よってこれをみたす点Pは存在しないからC4も表す図形なしである。
したがって、a>c>0 のとき
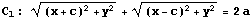
と
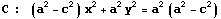
は同じ図形を表し、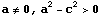 だから
だから
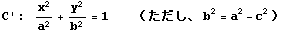
が表す図形も同じである。
つまりこのことによって、C'上のすべての点は2定点までの距離の和が一定になってることもわかった。
(2) 2定点からの距離の差が一定である点の軌跡
次に、 c>a>0 のとき
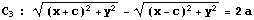
と
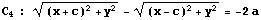
を合わせたものが
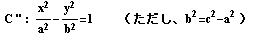
と同じ図形を表すことを確認する。
先ほどと同様にCは、C1, C2, C3, C4の和集合と同値であるが、明らかにC2の表す図形はない。
またc>a>0より、C1も

だから表す図形なし。
よって、CのグラフはC3,C4を合わせたものである。
c>a のとき、Cは
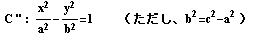
と同値だから、C"もC3,C4を合わせたものであるといえる。
また、c>0 より
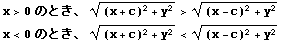
よって、C"のグラフの x>0の部分がC3、x<0 の部分がC4である。
(3) まとめ
- 0<a<c のとき
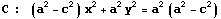
つまり
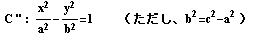
のグラフは
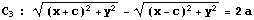
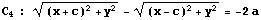
のグラフをあわせたものであり、x>0の部分がC3,x<0の部分がC4である。 - a=c のとき
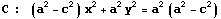
は
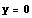
となる。すなわちx軸を表す。線分ABがC1,点Aの左側がC4,点Bの右側がC3である。[説明略] - a>c のとき
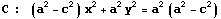
つまり
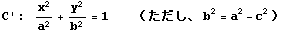
のグラフは
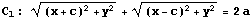
のグラフと同じである。