２つの円
　　　
　　　
までの接線の長さの和が一定(=2a)である点の軌跡の方程式は
　　　
である。ただし、a ,c,s,t>0とする。
　この式から２度の両辺二乗を経て根号を解消すると
　　　
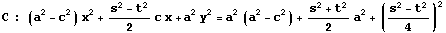
を得る。

２の(1)で述べたことと同様にして、C は
　　　
　　　
　　　
　　　
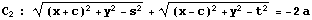
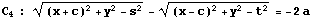
の和集合（”または”）と同値であることが証明される。（証明略）

C₂は明らかに表す図形なしである。C₁,C₃,C₄のグラフを合わせたものがCのグラフだと考えればよい。

（１） ２つの定円が共有点をもたない場合

２つの定円 A,Bが共有点をもたない、つまり
　　　
の場合を考える。
また、s≧t としておく。（ こうしても一般性を失わないだろう。）

上のように与えられた c,s,t に対して、定数 a の値を変化させてみる。
すると C の表す図形は、次の16とおりの場合に分けられる。（説明後述）

なおグラフは赤色の部分が C₁,青色の部分がC₃,緑色の部分がC₄である。

i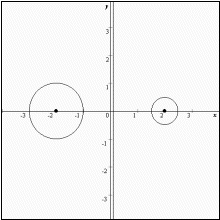
ii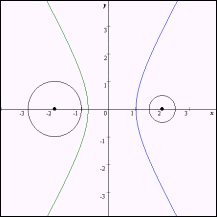
iii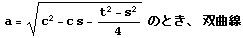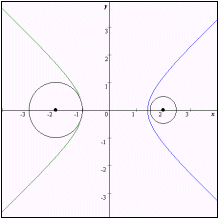
iv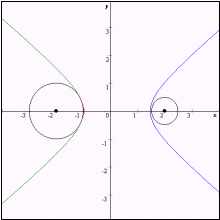
v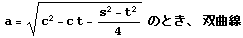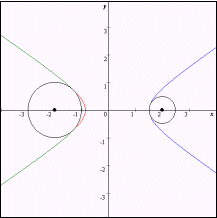
vi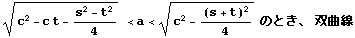
vii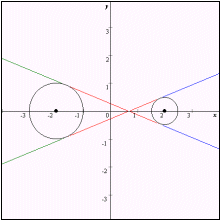
viii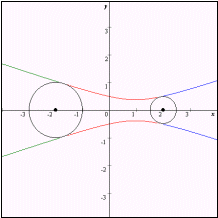
ix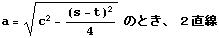
x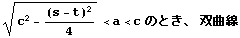
xi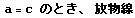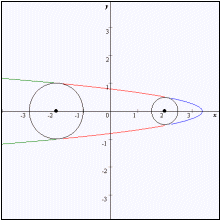
xii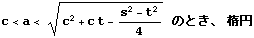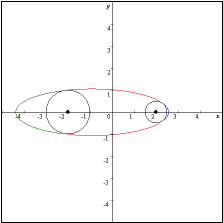
xiii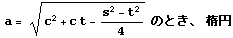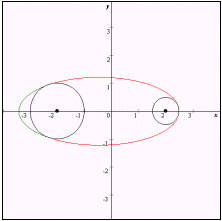
xiv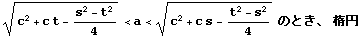
xv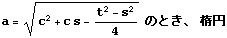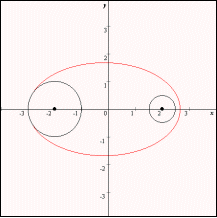
xvi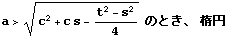

C の表す図形の分類は以上である。