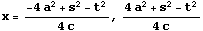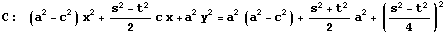
は、a≠0,a≠c のとき
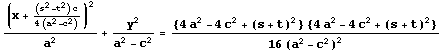
と変形できる。
この式の形から C の表す図形の種類が次のように分類できる。
[説明1] a の値による場合分けについて
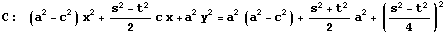
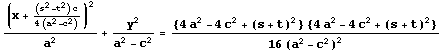
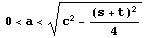 のとき 左右型の双曲線
のとき 左右型の双曲線
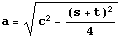 のとき 交わる2直線
のとき 交わる2直線
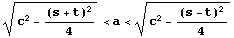 のとき 上下型の双曲線
のとき 上下型の双曲線
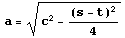 のとき 交わる2直線
のとき 交わる2直線
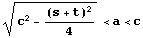 のとき 左右型の双曲線
のとき 左右型の双曲線
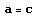 のとき 放物線
のとき 放物線
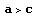 のとき 楕円
のとき 楕円
また C が定円 A と共有点をもつのは
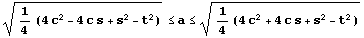
のときであり、それ以外のときは共有点なし。
また C が定円 B と共有点をもつのは
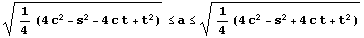
のときであり、それ以外のときは共有点なし。
また、s+t<2 c,s≧t より
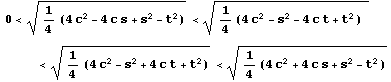
が保証されている。
よって、上のように 16の場合に分類した。
また C と A あるいは C と B の連立方程式の解は、それぞれ重解が2個である。
だから共有点をもつとき、C のグラフは A や B と2点で接する。
[説明2]C1,C3,C4の分離
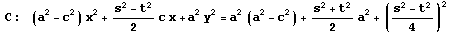
より
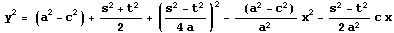
これをC1,C3,C4に代入したものを考えてみる。
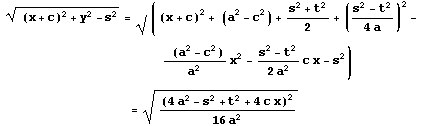
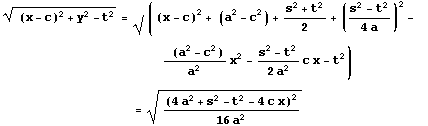
これらを x の関数とみたとき、グラフの概形は下図ようになる。
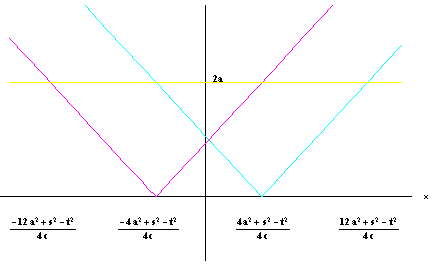
ただし、
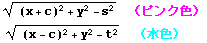
である。
このことから
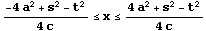
のとき
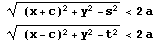
だから
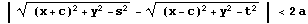
つまり、C3,C4はありえない。
よって(もしこの範囲にCのグラフが存在するなら)C1が対応している。
また
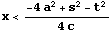
のとき
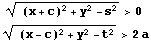
だから
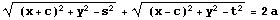
つまり、C1はありえない。
また
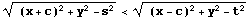
だからC3もありえない。
よって(もしこの範囲にCのグラフが存在するなら)C4が対応している。
同様にして
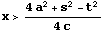
のときは、C3が対応している。
[まとめ]
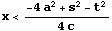 の部分には、C4
の部分には、C4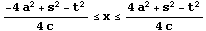 の部分には、C1
の部分には、C1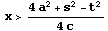 の部分には、C3
の部分には、C3