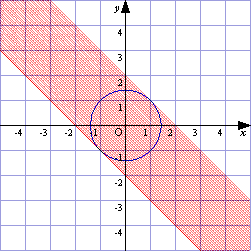
| ▼例題2 x2+y2=1,y=2x+k | |
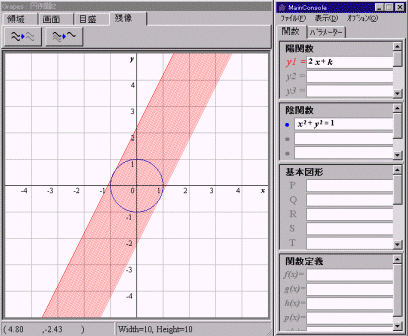 |
|
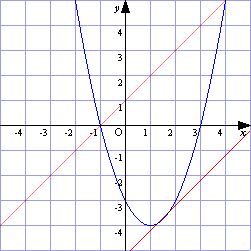
| ▼問7 x2+y2=2,y=-x+k | ▼練習3 y=x2-2x-3,y=x+k |
 |
 |
| A 平成10年度 数学Ⅱ「平面図形と式」(円と直線) |
| 日時 | 平成10年10月28日 水曜日 2校時 9:55~10:45 |
| 教科・科目 | 数学・数学Ⅱ |
| 教科書 | 啓林館 |
| 単元名 | 第1章 図形と方程式 |
| 単元目標 | 数学Ⅰの「2次関数」では,式で表された関数関係を,図形として表現し,その性質を調べてきた。この単元では,これとは逆に,図形を,適当な座標平面上におくことによって,その図形上の点の座標が満足する関係式(方程式または不等式)で表し,図形の性質を方程式・不等式の性質として調べる,いわゆる解析幾何学の方法を学ぶことを目標とする。 |
| 使用ソフト | GRAPES 5.40 |
| 使用場所 | 3F数学教室(コンピュータ室) |
| 使用台数 | 2人に1台 |
| 教科担任名 | 時岡郁夫 |
| 授業対象者 | 第2学年3組 37名(男子15名,女子22名) 文Ⅱコース |
| 全体指導時間 | 28時間 |
| 学習プリント | コンピュータを使用する時間には,練習問題とその結果を記入するプリントを配布し,コンピュータによる結果と計算による結果を後で比較できるようにする。 |
| 単元の構成 | (教)は普通教室 (コ)はコンピュータ室 |
| ○第1・2時(教) | 点と座標(その1) 直線上の点の座標 |
| ○第3~6時(教) | 点と座標(その2) 平面上の点の座標 |
| ○第7・8時(教) | 直線の方程式(その1) 直線の方程式のいろいろな形 |
| ○第9~11時(教) | 直線の方程式(その2) 2直線の位置関係(平行・垂直条件,点と直線との距離) |
| ○第12時(コ) | 直線の方程式(その3) 2直線の位置関係 コンピュータを用いて,方程式4x+3y+12+k(x-2y-2)=0 が定点を通る直線であることを確認させ,他の問題についても調べさせる。 |
| ○第13時(教) | 直線の方程式(その4) 問題演習 |
| ○第14時(教) | 円と直線(その1) 円の方程式を導き,基本的な円の方程式を求める。 |
| ○第15時(コ) | 円と直線(その2) コンピュータを用いて, x2+y2+lx+my+n=0の形の方程式がどのような図形を表すかを確認させる。 |
| ○第16時(教) | 円と直線(その3) 3点を通る円の方程式を求める。 |
| ○第17時(教) | 円と直線(その4) 円と直線との位置関係 円と直線との共有点の座標を求めることにより,円と直線の位置関係をとらえる。 |
| ○第18時(コ) (本時) |
コンピュータで円x2+y2=1と直線y=2x+kの,kの値をいろいろ変化させたグラフを描き,位置関係をとらえる。放物線と直線についても調べさせる。 |
| ○第19時(教) | 第18時の結果を,実際に計算によって求めることで確認させ,定着を図る。 |
| ○第20・21時(教) | 円の接線,問題演習 |
| ○第22~24時(教) | 軌跡と領域(その1) 軌跡 |
| ○第25~28時(教) | 軌跡と領域(その2) 不等式の表す領域(必要に応じてコンピュータを用いる) |
| 本時の目標 |
|
| 指導過程 |
| ねらい |
学習活動 (→:指示・説明[教師],⇒発問・活動[生徒]) |
指導上の留意点および評価
(○:留意点,□評価) |
| 導入・前時の復習 | →コンピュータを起動し,教科書の問5を入力しなさい。 | |
|
⇒コンピュータを起動し,GRAPESを呼び出す。 ⇒問5(x2+y2=5とy=2x+5)の円の方程式,直線の方程式を入力する。 (問5は,前時に解説済み) |
○直線は「陽関数」,円は「陰関数」で入力することを注意する。 | |
| ⇒コンピュータの解答と前時の解答を比較・確認する。→PCゼミで,生徒の取り組み状況について確認する。 |
(□関心・意欲) 意欲的に取り組んでいるか。 |
|
| 展開1・例題2を解答する |
→画面を初期化し,例題2を入力しなさい。 →GRAPESのパラメータkの値を変えて入力し,円と異なる2点で交わるときのkの値の範囲を調べなさい。 |
○画面を初期化する。 ○関数の入力場所を指示する。 ○パラメータ変更方法を指示する。 |
|
⇒例題2(x2+y2=1とy=2x+k)を入力する。 ⇒GRAPESのパラメータの画面を選択する。 ⇒パラメータkを変え,直線と円が異なる2点で交わるものを探す。 |
(□表現・処理) 関数・パラメータを正しく入力できるか。 kの範囲を求められるか (□数学的な考え方) kの変化がグラフにおいてどのような意味を持つか理解できるか。 |
|
| 展開2・問7,練習3問7,練習3を解答するを解答する | →画面を初期化し,問7,練習3を解答しなさい。 | |
| ⇒問7(x2+y2=2とy=-x+k)を入力,解答をコンピュータから読み取る。 |
(□知識・理解) 適切に入力できたか。 (□表現・処理) kの範囲がある程度正しく言えるか。 |
|
| ⇒練習3(y=x2-2x-3とy=x+k)を入力,解答をコンピュータから読み取る。 |
(□数学的な考え方) 円の場合と放物線の場合の類似性に気づくか。 |
|
| 展開3・問題演習 | ⇒学習プリント(別紙)問題を入力,解答をコンピュータから読み取る。 |
(□関心・意欲) 意欲的に取り組んでいるか。 (□表現・処理) 関数・パラメータを正しく入力できるか。 kの範囲を求められるか。 |
| 本時まとめ・次時の予告 |
→コンピュータを使うことで,図形の問題を具体的に見ながら考えていくことが有効であることを強調する。 次時は,「計算で求めること」を予告する。 |
○時間内に終了できないものについて,放課後などに学習することを指示する。 |
| ▼例題2 x2+y2=1,y=2x+k | |
 |
|
| ▼問7 x2+y2=2,y=-x+k | ▼練習3 y=x2-2x-3,y=x+k |
 |
 |
|
1. 次の円と直線について問に答えよ。 (1) x2+y2=10,y=-x+k ① k=5のとき,共有点は何個か。 ② 接するときのkの値を求め,そのときの接点の座標を求めよ。 ③ kの値が変化すると,直線はどのような変化を見せるか考えよ。
|
|
(2) x2+y2=k(k>0),y=3x-4 ① k=2のとき,共有点は何個か。 ② 異なる2点で交わるときのkの値の範囲を求めよ。 ③ kの値が変化すると,円はどのような変化を見せるか考えよ。
|
|
(3) x2+y2-x+4y=0,y=kx+2 ① k=2のとき,共有点は何個か。 ② 接するときのkの値を求めよ。 ③ kの値が変化すると,直線はどのような変化を見せるか考えよ。
|
|
2. 放物線y=x2+kx+1と直線y=x-1が接するとき,kの値を求めよ。また,そのときの接点の座標を求めよ。
|
● 回収した学習プリントの解答結果から
(1) ③ 直線y=-x+kで,kの値が変化すると,直線はどのような変化を見せるか考えよ。
(2) ③ 円x2+y2=k(k>0)で,kの値が変化すると,円はどのような変化を見せるか考えよ。
(3) ③ 直線y=kx+2で,kの値が変化すると,直線はどのような変化を見せるか考えよ。
【解説】
(1) ③ 直線y=-x+kは,傾きが一定(-1)の直線であるから,kの値が変化すると,直線は平行移動する。
● 最後に,