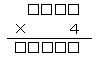
(1) f(x) 傪場悢暘夝偣傛丏
(2) 曽掱幃 f(x)=0 傪夝偗丏
丂丂丂
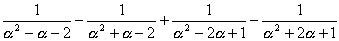
丂丂丂
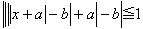
偼 -1亝x亝1偺偲偒丆忢偵惉傝棫偮偲偄偆丏偙偺偲偒丆揰 (a,b) 偺懚嵼偡傞斖埻傪恾帵偣傛丏
丂丂丂D=(兛-兝)2(兝-兞)2(兞-兛)2
(1) a,b,c 傪 n,p 偱昞偣丏
(2) a,b,c 偺娭學幃傪媮傔傛丏
(1) x3-3x+1=0
(2) x3+x2-2x-1=0
(3) x3+x2-4x+1=0
(4) x3+x2-6x-7=0
丂丂丂
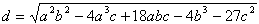
偑桳棟悢偱偁傞偲偡傞丏偙偺偲偒丆曽掱幃 f(x)=0 偺侾偮偺夝傪兤偲偡傞偲偒丆懠偺夝傪兤偺嵟掅師偺惍幃偲偟偰昞偣丏
丂丂丂
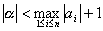
偱偁傞偙偲傪徹柧偣傛丏
丂丂丂13579x-97531y=k (掕悢)
傪夝偗丏
丂丂丂1222x-8777y=1
偱偁偭偨丏k 偺抣傪媮傔傛丏
(1) x乥y-4乥+y乥x+2乥=2 偺僌儔僼傪偐偗丏
(2) x 偵娭偡傞曽掱幃 乥a-4乥x+a乥x+2乥=2 偵偮偄偰丆
丂嘆 惓偺夝傪傕偮偲偒偺 a 偺抣偺斖埻傪媮傔傛丏
丂嘇 俀偮偺夝傪傕偮偲偒偺 a 偺抣偺斖埻傪媮傔傛丏
丂嘊 嘇偱俀偮偺夝偺嵎偑嵟彫偲側傞偲偒偺 a 偺抣傪媮傔傛丏
(1) [x]2-3x+2亙0
(2) [x2]-3x+2亙0
(3) [x2]-[3x]+2亙0
丂丂丂
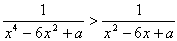
傪夝偗丏偨偩偟丆a 偼幚悢丏
丂丂丂
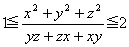
傪徹柧偣傛丏偨偩偟丆a,b,c 偼幚悢偱丆abc亗0 偲偡傞丏
(1) N 傪媮傔傛丏
(2) N亙n/4 傪徹柧偣傛丏
(1)
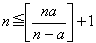 傪徹柧偣傛丏
傪徹柧偣傛丏(2)
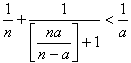 傪徹柧偣傛丏
傪徹柧偣傛丏
丂丂丂f(x)=(x-兝1)(x-兝2)(x-兝3)
傪媮傔傛丏
丂丂丂兝i=兛i+兛-i丆兞1=兝1+兝5丆兞2=兝2+兝3丆兞3=兝4+兝6
偲偍偔偲偒丆懡崁幃
丂丂丂f(x)=(x-兞1)(x-兞2)(x-兞3)
傪媮傔傛丏
丂丂丂兝i=兛i+兛-i丆
丂丂丂兞1=兝1+兝7+兝8丆兞2=兝2+兝3+兝5丆兞3=兝4+兝6+兝9
偲偍偔偲偒丆懡崁幃
丂丂丂f(x)=(x-兞1)(x-兞2)(x-兞3)
傪媮傔傛丏
丂丂丂兝1=(兛1+兛2)(兛3+兛4), 兝2=(兛1+兛3)(兛2+兛4),兝3=(兛1+兛4)(兛2+兛3)
丂丂丂兞1=兝12兝2+兝22兝3+兝32兝1, 兞2=兝1兝22+兝2兝32+兝3兝12
偲偍偔偲偒丆師偺栤偄偵摎偊傛丏
(1) 兝1, 兝2, 兝3 傪俁偮偺夝偵傕偪丆x3 偺學悢偑侾偱偁傞俁師曽掱幃傪 g(x)=0 偲偡傞丏g(x) 傪媮傔傛丏
(2) 兞1, 兞2 傪俀偮偺夝偵傕偪丆x2 偺學悢偑侾偱偁傞俀師曽掱幃傪 h(x)=0 偲偡傞丏h(x) 傪媮傔傛丏
(3) f(x),g(x),h(x) 偺敾暿幃傪偦傟偧傟 d(f),d(g),d(h) 偲偍偔偲偒丆
丂丂丂d(f)=d(g)=d(h)
傪徹柧偣傛丏偨偩偟丆敾暿幃偲偼夝偺嵎愊偺暯曽偱丆椺偊偽丆d(g)=(兝1-兝2)2(兝2-兝3)2(兝3-兝1)2 偱偁傞丏
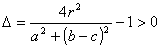 偲偡傞丏
偲偡傞丏
(1) 1+sin兤=tan兤 偺偲偒丆sin兤 偺抣傪媮傔傛丏
(2) 1-sin兤=tan兤 偺偲偒丆sin兤 偺抣傪媮傔傛丏
(3) 1+cos兤=tan兤 偺偲偒丆cos兤 偺抣傪媮傔傛丏
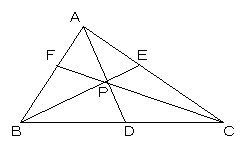
丂丂丂
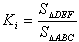
偺抣傪媮傔傛丏
(1) K1 偼揰 P 偑廳怱偺応崌
(2) K2 偼揰 P 偑撪怱偺応崌
(3) K3 偼揰 P 偑奜怱偺応崌
(4) K4 偼揰 P 偑悅怱偺応崌
(5) K5 偼揰 D,E,F 偑撪愙墌偺愙揰偺応崌
(1) BD,CD 偺挿偝傪媮傔傛丏
(2) 仮DEF 偺柺愊 K 傪媮傔傛丏偨偩偟丆仮ABC 偺柺愊傪 S 偲偡傞丏
(3) K 偺嵟戝抣傪梌偊傞 x,y 偺抣傪媮傔傛丏傑偨丆偙偺偲偒揰P 偼偳傫側揰偐丏
(1) 慄暘 AA', BB', CC' 偼侾揰 P 偱岎傢傞偙偲傪徹柧偣傛丏
(2) AP 偺挿偝傪媮傔傛丏
(3) AP2+BP2+CP2 傪媮傔傛丏
丂丂丂
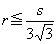
傪徹柧偣傛丏
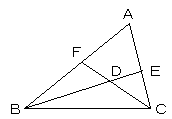
(1) A=60亱偱揰D 偑撪怱側傜偽丆DE=DF
(2) AB亗AC丆揰D 偼撪怱丆DE=DF 側傜偽丆巐妏宍 ABCD 偼墌偵撪愙偡傞丏
丂丂丂AB=b, AD=d, AE=e, AC=c
偲偍偔偲偒丆師偺栤偄偵摎偊傛丏
(1) bc=bd+de+ec 傪徹柧偣傛丏
(2) e/b+d/c 偺嵟彫抣傪媮傔傛丏
(1) a=m2-mn+n2, b=2mn-n2, c=m2-n2
(2) a=m2+mn+n2, b=2mn+n2, c=m2-n2
丂丂丂AD=nAC (0亙n亙1), AE=mAB (0亙m亙1)
偲偍偔偲偒丆柺愊斾
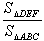 傪媮傔傛丏
傪媮傔傛丏
(1) x, y, z 偺娭學幃傪媮傔傛丏
(2) AE丗EB亖k丗1 偲偍偔偲偒丆k偺抣傪 x, y 傪梡偄偰昞偣丏
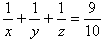 傪枮偨偡帺慠悢 x,y,z (x亝y亝z) 偺抣傪媮傔傛丏
傪枮偨偡帺慠悢 x,y,z (x亝y亝z) 偺抣傪媮傔傛丏
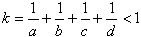 傪枮偨偟偰偄傞丏k 偺嵟戝抣偲丆偦偺偲偒偺 a,b,c,d 偺抣傪媮傔傛丏
傪枮偨偟偰偄傞丏k 偺嵟戝抣偲丆偦偺偲偒偺 a,b,c,d 偺抣傪媮傔傛丏
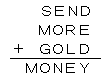
(1) 係偮悢 1777丆7177丆7717丆7771 偺拞偱丆慺悢偱側偄悢偼偳傟偐丏
(2) 俆偮悢 17777丆71777丆77177丆77717丆77771 偺拞偱丆慺悢偼偳傟偐丏
(3) 俈偮悢 1777777丆7177777丆7717777丆7771777丆7777177丆7777717丆7777771 偺拞偱丆17 傪場悢偵傕偮悢偼偳傟偐丏
(4) 俉偮悢 17777777丆71777777丆77177777丆77717777丆77771777丆77777177丆77777717丆77777771 偺拞偱丆慺悢偼偳傟偐丏
(1)

(2)
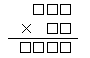
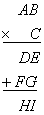
丂丂丂
丂丂丂