(1) (x4-4x2-4)2
(2)

F1=3(b+c)(c+a)(a+b)
F2=5(b+c)(c+a)(a+b)(‡”a2+‡”ab)
F3=7(b+c)(c+a)(a+b)(‡”a4+2‡”a3b+3‡”a2b2+5‡”a2bc)
F4=3(b+c)(c+a)(a+b)(3‡”a6+9‡”a5b+19‡”a4b2+35‡”a4bc+23‡”a3b3+63‡”a3b2c)
F5=11(b+c)(c+a)(a+b)(‡”a8+4‡”a7b+11‡”a6b2+21‡”a6bc+9‡”a5b3+54‡”a5b2c+23‡”a4b4+84‡”a4b3c+123‡”a4b2c2+159‡”a3b3c2)
2
 Ѓ@Ѓi•њҚ†“ҮЏ‡Ѓj
Ѓ@Ѓi•њҚ†“ҮЏ‡Ѓj
p2q2-4p3r+18pqr-4q3-27r2
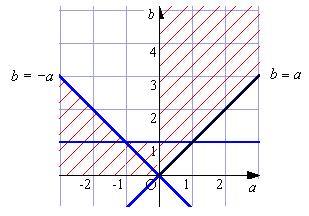
(1) a=-3n+p, b=3n2-2np-1, c=-n3+n2p+n-p
(2) 4a4-a2b2+4a3c-24a2b+4b3-18abc-32a2+36b2+27c2+96b+64=0
(1) -ѓЖ2-ѓЖ+2, ѓЖ2-2
(2) -ѓЖ2-ѓЖ+1, ѓЖ2-2
(3) -ѓЖ2-2ѓЖ+2, ѓЖ2+ѓЖ-3
(4) -ѓЖ2+4, ѓЖ2-ѓЖ-5
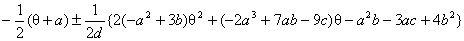
D=(a-b-p+q)2+4pqЃ†0
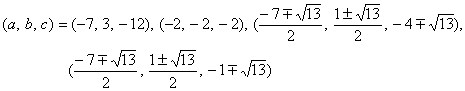 Ѓ@Ѓi•њҚ†“ҮЏ‡Ѓj
Ѓ@Ѓi•њҚ†“ҮЏ‡Ѓj
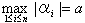 ‚Ж‚Ё‚‚ЖЃC|ѓүi|Ѓ…aЃ@(i=1,2,Ѓc,n)
‚Ж‚Ё‚‚ЖЃC|ѓүi|Ѓ…aЃ@(i=1,2,Ѓc,n)|ѓү|Ѓ†a+1 ‚Ж‰ә’и‚µ‚ДЃC–µЏ‚‚𓱂ЃB
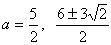
x=31t+12k, y=13t+5k (t‚Нђ®ђ”)Ѓ@‚ж‚иЃCk=2, 3
x=97531t+8777k, y=13579t+1222k (t‚Нђ®ђ”)
k=6, 7, 8, Ѓc,16
(1) ‡@xЃ†-2, yЃ†4‚М‚Ж‚«Ѓ@Ѓ@(x+1)(y-2)=-1
Ѓ@Ѓ@‡AxЃѓ-2, yЃ†4‚М‚Ж‚«Ѓ@Ѓ@y=-2x-1
Ѓ@Ѓ@‡BxЃѓ-2, yЃѓ4‚М‚Ж‚«Ѓ@Ѓ@(x+1)(y-2)=-3
Ѓ@Ѓ@‡CxЃ†-2, yЃѓ4‚М‚Ж‚«Ѓ@Ѓ@y=-2x+1
(2) ‡@ aЃѓ1Ѓ@Ѓ@‡A aЃ„2Ѓ@Ѓ@‡B a=4
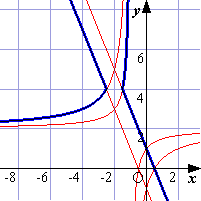
(1) 2/3ЃѓxЃѓ1, 1ЃѓxЃѓ2, 2ЃѓxЃѓ3, 11/3ЃѓxЃѓ4
(2) 2/3ЃѓxЃѓ1, 1ЃѓxЃѓ2, 2ЃѓxЃѓЃг5, 7/3ЃѓxЃѓЃг6
(3) 4/3Ѓ…xЃѓЃг2, 5/3Ѓ…xЃѓЃг3
(±) aЃ…-27‚М‚Ж‚«
Ѓ@Ѓ@Ѓ@
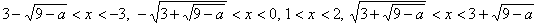
(І) -27ЃѓaЃ…0‚М‚Ж‚«
Ѓ@Ѓ@Ѓ@
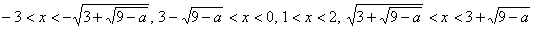
(і) 0ЃѓaЃ…5‚М‚Ж‚«
Ѓ@Ѓ@Ѓ@

(ө) 5ЃѓaЃ…8‚М‚Ж‚«
Ѓ@Ѓ@Ѓ@
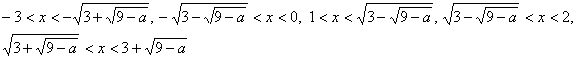
(µ) 8ЃѓaЃ…9‚М‚Ж‚«
Ѓ@Ѓ@Ѓ@
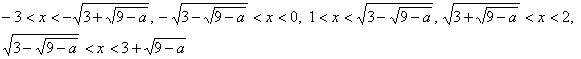
(¶) 9Ѓѓa‚М‚Ж‚«
Ѓ@Ѓ@Ѓ@
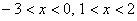
2(yz+zx+xy)-(x2+y2+z2)=3(bc+ca+ab)2Ѓ†0
x2+y2+z2-(yz+zx+xy)=(a+b+c)2{(b-c)2+(c-a)2+(a-b)2}/2Ѓ†0
(1)
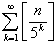
(2) [x]Ѓ…x ‚рҺg‚¤
ЏИ—Ғ
x3+x2-2x-1
x3+x2-4x+1
x3+x2-6x-7
(1) g(x)=x3-2px2+(p2-4r)x+q2
(2) h(x)=x2+(-2p3+8pr-3q2)x+p6-12p4r+4p3q2+48p2r2-48pq2r-64r3+9q4
(3) ЏИ—Ғ
1/4 (x=-1, y=-1/2)
 Ѓ@Ѓi•њҚ†“ҮЏ‡Ѓj
Ѓ@Ѓi•њҚ†“ҮЏ‡Ѓj
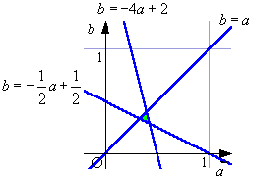
(1)
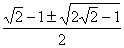
(2)

(3) -1,
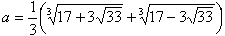 Ѓ@Ѓia3+a2+a-1=0 ‚МҺАђ”‰рЃj
Ѓ@Ѓia3+a2+a-1=0 ‚МҺАђ”‰рЃj
(1) 1/4
(2)

(3)

(4)
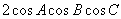
(5)
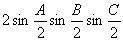
(1)
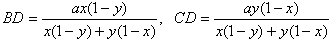
(2)

(3) KЃ…S/4, x=y=1/2Ѓ@(“™Қ†‚Н“_P‚ҒЃұABC‚МЏdђS‚М‚Ж‚«)
(1) ЃЪAPC'=ЃЪC'PB=ЃЪBPA'=ЃЪA'PC=ЃЪCPB'=ЃЪB'PA=60Ѓ‹‚рҺ¦‚·ЃB
(2)
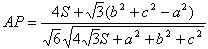
(3)
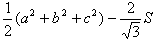
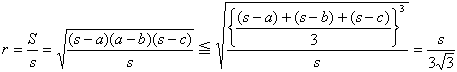
‹¤’К“ађЪђьЃ@Ѓ@Ѓ@

‹¤’КЉOђЪђьЃ@Ѓ@Ѓ@
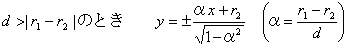
(1) ЃЪEDC=60Ѓ‹ЃЁЃұFDE‚Н‰~‚Й“ађЪЃЁЃұDEF‚Н“с“™•УҺOЉpЊ`
(2) ЃЪAFD=ѓүЃCЃЪAED=ѓА
Ѓ@ђіЊ·’и—қ‚ж‚и
Ѓ@Ѓ@Ѓ@
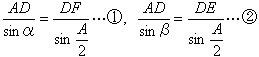
Ѓ@‡@ЃC‡A‚Ж‰ә’и‚ж‚и
Ѓ@Ѓ@Ѓ@sinѓү=sinѓА
Ѓ@Ѓ@Ѓ@Ѓ@Ѓ€ѓү+ѓА=ѓОЃ@orЃ@ѓү=ѓА
Ѓ@ѓүЃ‚ѓА‚ж‚и
Ѓ@Ѓ@Ѓ@ѓү+ѓА=ѓО
Ѓ@‚䂦‚Й‰~‚Й“ађЪ‚·‚й
(1) ЏИ—Ғ
(2) 2(Ѓг2-1)Ѓ@“™Қ†‚Нd=e‚М‚Ж‚«
(1) A=60Ѓ‹
(2) A=120Ѓ‹

(1) 2z2=x2+y2
(2)

m>n, (m,n)=1 ‚Ж‚µ‚ДЏ‡‚Й
Ѓ@Ѓ@Ѓ@m2n, m3, n3, n(m2-n2), mn2, m(m2-n2)
Ѓ@Ѓ@Ѓ@<3, 1>=9, 27, 1, 8, 3, 24
Ѓ@Ѓ@Ѓ@<3, 2>=18, 27, 8, 10, 12, 15
Ѓ@Ѓ@Ѓ@<4, 1>=16, 64, 1, 15, 4, 60
Ѓ@Ѓ@Ѓ@<4, 3>=48, 64, 27, 21, 36, 28
(x, y, z)=(2, 3, 15)
k=1805/1806, a=2, b=3, c=7, d=43
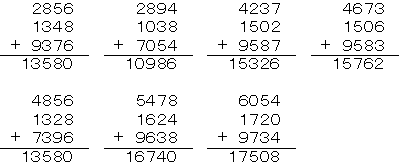
(1) 7771=19Ө409
(2) 71777
(3) 7777177=17Ө331Ө1471
(4) 77777177
(1)
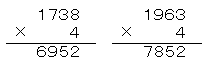
(2)
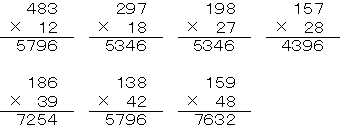
1968 (43) 5, 27 (‰О)
1968 (43) 7, 25 (‹а)
1973 (48) 6, 25 (ЊҺ)
1973 (48) 5, 26 (“y)
1978 (53) 4, 26 (ђ…)
1978 (53) 6, 24 (“y)
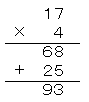
21978Ѓ~4ЃЃ87912
1738Ѓ~4ЃЃ06952ЃC1963Ѓ~4ЃЃ07852ЃC3907Ѓ~4ЃЃ15628ЃC
7039Ѓ~4ЃЃ28156ЃC9127Ѓ~4ЃЃ36508