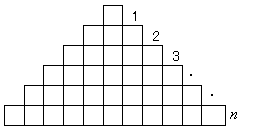(1) sin3兛+sin3兝+sin3兞=-12sin兛sin兝sin兞=3sin(兛+兝+兞) 傪徹柧偣傛丏
(2) cos3兛+cos3兝+cos3兞=12cos兛cos兝cos兞=3cos(兛+兝+兞) 傪徹柧偣傛丏
(3) (1+cos兛cos兝)2+(1+cos兝cos兞)2+(1+cos兞cos兛)2 偺抣傪媮傔傛丏
(1) 佢ABD=20亱, 佢DBC=60亱, 佢BCA=50亱, 佢ACD=30亱
(2) 佢ABD=20亱, 佢DBC=60亱, 佢BCA=30亱, 佢ACD=50亱
(1) fn(x) 偼 x2+1 傪場悢偵傕偮偙偲傪徹柧偣傛丏
(2) 偡傋偰偺幚悢x偵懳偟偰丆f4(x)>0 偲側傞傛偆偵丆sin兤 偺抣偺斖埻傪媮傔傛丏
丂丂丂z=a sin x sin y+b sin x cos y+c cos x sin y+d cos x cos y
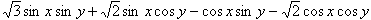 偺嵟戝丒嵟彫抣傪媮傔傛丏
偺嵟戝丒嵟彫抣傪媮傔傛丏偨偩偟丆
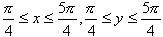 偲偡傞丏
偲偡傞丏
(1) x3+y3+z3-3xyz 傪 x丆y丆z偺1師幃偺愊偺宍偵昞偣丏
(2) 俁師曽掱幃 x3-3uvx+u3+v3=0 傪夝偗丏
(3) 俁師曽掱幃 x3+ax+b=0 傪夝偗丏
(4) 俁師曽掱幃 x3+px2+qx+r=0 偺夝朄傪弎傋傛丏
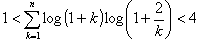 傪枮偨偡n偺抣偺屄悢傪媮傔傛丏
傪枮偨偡n偺抣偺屄悢傪媮傔傛丏
(1) 0亙兛亙x亝兝偱丆忋偺娭學傪枮偨偡x偑懚嵼偡傞偨傔偺兛, 兝, k 偺忦審傪媮傔傛丏
(2)
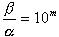 (m偼惓偺惍悢)偺偲偒丆忋偺娭學傪枮偨偡x偺抣偺屄悢傪媮傔傛丏
(m偼惓偺惍悢)偺偲偒丆忋偺娭學傪枮偨偡x偺抣偺屄悢傪媮傔傛丏(3) 忋偺娭學傪枮偨偡x偺抣偑n屄偁傝丆彫偝偄傕偺偐傜弴偵暲傋偰丆i 斣栚偺 x 偺抣傪 xi 偲偍偔偲偒丆xi 傪 兛, k, i 傪梡偄偰昞偣丏
(4) (3)偱丆
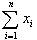 傪媮傔傛丏
傪媮傔傛丏
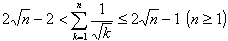 傪徹柧偣傛丏
傪徹柧偣傛丏
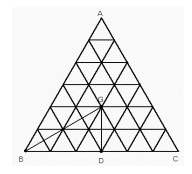
(1) 戝彫偡傋偰偺惓嶰妏宍偺屄悢傪媮傔傛丏
(2) 惓嶰妏宍俙俛俠偺廳怱傪俧丆俛俠偺拞揰傪俢偲偡傞偲偒丆嚈俧俛俢偵娷傑傟傞奿巕揰偺屄悢傪媮傔傛丏
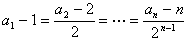 偺偲偒丆
偺偲偒丆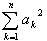 偺嵟彫抣傪媮傔傛丏
偺嵟彫抣傪媮傔傛丏
(1)
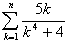
(2)
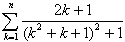
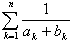 傪媮傔傛丏
傪媮傔傛丏丂丂丂{an}丗a1=-18, a2=-23, an+2=2an+1-an+2n
丂丂丂{bn}丗b1=24, bn+1=2bn-n3
丂丂丂
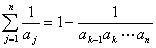
傪徹柧偣傛丏偨偩偟丆 n亞k-1 偲偡傞丏
a(k-1)n+1-a(k-1)n=a(k)n (k=1,2,乧,m), a(m)n+1-a(m)n=0 偺偲偒丆
丂丂丂
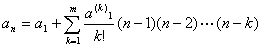
傪徹柧偣傛丏
(1)
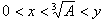 偺偲偒丆
偺偲偒丆丂丂丂
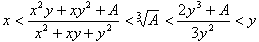
傪徹柧偣傛丏
(2)
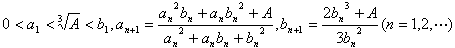
偲偍偔偲偒丆俀偮偺嬌尷抣
丂丂丂
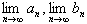
傪媮傔傛丏
(1) a0 偺抣傪媮傔傛丏
(2) a-n=an 傪徹柧偣傛丏
(3) an+7m=an 傪徹柧偣傛丏
(4) 偡傋偰偺 an 偼丆a0,a1,a2,a3 偺偄偢傟偐偵摍偟偄偙偲傪徹柧偣傛丏
(5) a1=a 偲偍偔偲偒丆a2, a3, a4 傪 a 偱昞偣丏
(6) x=a 傪侾偮偺夝偵傕偮丆嵟掅師偺桳棟悢學悢偺曽掱幃 f(x)=0 傪媮傔傛丏偨偩偟丆懡崁幃 f(x) 偺嵟崅師偺崁偺學悢偼侾偱偁傞丏
(7) f(an) 偺抣傪媮傔傛丏
(8)
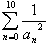 偺抣傪媮傔傛丏
偺抣傪媮傔傛丏(9) an 傪 a 偺嵟掅師偺桳棟悢學悢偺懡崁幃偲偟偰昞偣丏
(1) 俠偺嬌抣傪媮傔傛丏
(2) 俠偑尨揰偱懳徧偵側傞傛偆偵丆p, q 偺抣傪媮傔傛丏
(3) 俠偑尨揰傪捠傝丆嬌戝抣偑侽偲側傞傛偆偵丆p, q 偺抣傪媮傔傛丏
(4) 俠偑捈慄 y=9x 偵愙偟丆嬌彫抣偑侽偲側傞傛偆偵丆p, q 偺抣傪媮傔傛丏
(1) an+3-3an+1+an+2=0 傪徹柧偣傛丏
(2) a10 偺抣傪媮傔傛丏
丂丂丂x3+ax2+ax+a=0丂乧嘆丆
丂丂丂x3+ax2+ax-a=0丂乧嘇丆
丂丂丂x3+ax2-ax+a=0丂乧嘊丆
丂丂丂x3+ax2-ax-a=0丂乧嘋
偵偮偄偰丆師偺栤偄偵摎偊傛丏偨偩偟丆a 偼侽偱側偄掕悢偲偡傞丏
(1) 憡堎側傞俁偮偺幚悢夝傪傕偮偙偲偑偱偒傞曽掱幃偼偳傟偐丏傑偨偦傟偼偳偺傛偆側a偺抣偺偲偒偐丏
(2) 嘆乣嘋偡傋偰偺曽掱幃偑丆幚悢夝傪傕偨側偄傛偆側a偺抣偺斖埻傪媮傔傛丏
(1) max(x, y, z)-min(x, y, z) 偺庢傝摼傞抣偺斖埻傪媮傔傛丏
(2) x3+y3+z3 偺庢傝摼傞抣偺斖埻傪媮傔傛丏
(1) 0亙x亙兾/2 偵偍偗傞y偺嵟彫抣偲丆偦偺偲偒偺x偺抣傪媮傔傛丏
(2) 兾/2亙x亙2兾 偵偍偗傞y偺嵟戝抣偲丆偦偺偲偒偺 sin x, cos x 偺抣傪媮傔傛丏
丂丂丂y=(sin x+cosec x)2+(cos x+sec x)2+(tan x+cot x)2
偺嵟彫抣偲丆偦偺偲偒偺x偺抣傪媮傔傛丏
丂丂丂
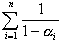
偺抣傪媮傔傛丏
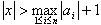 偺偲偒丆摍幃
偺偲偒丆摍幃 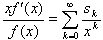 傪徹柧偣傛丏
傪徹柧偣傛丏
丂丂丂
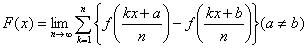
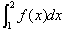 偺抣傪彫悢戞俀埵傑偱惓偟偔媮傔傛丏
偺抣傪彫悢戞俀埵傑偱惓偟偔媮傔傛丏偨偩偟丆f(1)=0 偲偡傞丏傑偨丆x3-x-1=0 偺幚悢夝傪兛偲偍偔偲偒丆兛=1.3247, 兛2+3兛=5.7290 偱偁傞丏
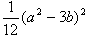 埲壓偱偁傞偙偲傪徹柧偣傛丏
埲壓偱偁傞偙偲傪徹柧偣傛丏
(1) 俁師曽掱幃 x3-3x+1=0 傪 x=r cos兤 (r亜0, 0亝兤亝兾)偲偍偄偰夝偗丏
(2) 嬋慄 y=x3-3x+1 偲x幉偲偱埻傑傟偨晹暘偺柺愊傪媮傔傛丏
丂丂丂
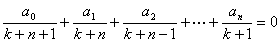
偺偲偒丆n師曽掱幃
丂丂丂a0xn+a1xn-1+a2xn-2+乧+an=0
偼丆侽偲侾偺娫偵彮側偔偲傕侾偮偺幚悢夝傪傕偮偙偲傪徹柧偣傛丏
(1) 揰Q偺婳愓偺曽掱幃傪媮傔傛丏
(2) 揰Q偺婳愓偲慄暘OB偵傛偭偰埻傑傟傞晹暘偺柺愊傪媮傔傛丏
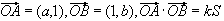 偺偲偒丆佢AOB 偺梋尫偺抣傪k傪梡偄偰昞偣丏偨偩偟丆S偼仮AOB偺柺愊偱偁傞丏
偺偲偒丆佢AOB 偺梋尫偺抣傪k傪梡偄偰昞偣丏偨偩偟丆S偼仮AOB偺柺愊偱偁傞丏
(1) 佢AOP=佢OBP
(2) 佢AOP=佢ABP
(1) FQ=1
(2) FQ=2
(3) FQ=3
(4) FQ=4
丂丂丂Ax2+2Hxy+By2=c
偲側偭偨丏偙偺偲偒丆師偺栤偄偵摎偊傛丏
(1) 師偺摍幃傪徹柧偣傛丏
丂丂丂A+B=a+b, AB-H2=ab-h2
(2) H=0 偲側傞傛偆偵丆夞揮妏兤傪掕傔傛丏
(3) (2)偺偲偒丆2h(a-b)亜0 傪徹柧偣傛丏
(1)
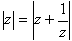
(2)
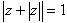
丂丂丂
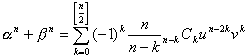
(1) 儚儞儁傾丂 
(2) 僣乕儁傾丂 
(3) 僗儕乕僇乕僪丂 
(4) 僗僩儗乕僩丂 
(5) 僼儔僢僔儏丂 
(6) 僼儖僴僂僗丂 
(7) 僼僅乕僇乕僪丂 
(8) 僗僩儗乕僩僼儔僢僔儏丂 
(9) 儘僀儎儖僗僩儗乕僩僼儔僢僔儏丂 
偙偺憖嶌傪m夞孞傝曉偟偨偲偒丆戃偺拞偵敀媴r屄巆偭偰偄傞妋棪 P(n,m,r) 傪媮傔傛丏偨偩偟丆敀媴丆崟媴偲傕摨宍摨幙偱丆戃偺拞偐傜偼摨掱搙偵慖偽傟傞傕偺偲偡傞丏
丂丂丂