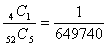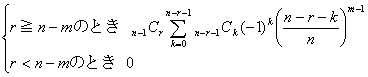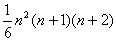(1)(2) z1=cosα+i sinα,z2=cosβ+i sinβ,z3=cosγ+i sinγとおくと,
z13+z23+z33=3z1z2z3
(3) 33/16
-1/8
(1) 30°
(2) 10°
√2/4,√2:1
(1) f(i)=0
(2) -√6/3<sinα<0, 0<sinα<√6/3
最大値
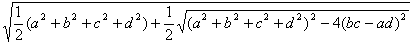
最小値
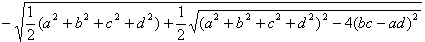
最大値
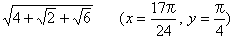
最小値
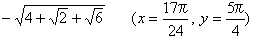
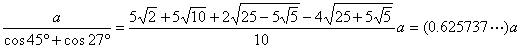
(1) (x+y+z)(x+ωy+ω2z)(x+ω2y+ωz) (ωは1の虚数立方根)
(2) x=-u-v, -ωu-ω2v, -ω2u-ωv
(3)
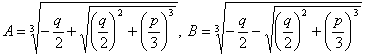 とおくと
とおくとx=A+B, ωA+ω2B, ω2A+ωB
(4) x=ξ-p/3 とおくと,ξ3+aξ+b=0 (ただし,a=-p2/3+q, b=2p3/27-pq/3+r)
9≦n≦98 90個
(1)
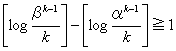
(2) m(k-1)
(3)
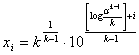
(4)
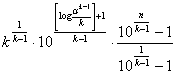
以下略
(1)
(2)
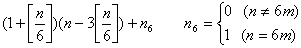
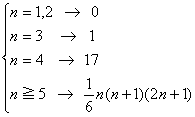
p → an
0 → 1+2n-1(a-1)
1 → n+1+2n-1(a-2)
2 → n2+2n+3+2n-1(a-6)
3 → n3+3n2+9n+13+2n-1(a-26)
4 → n4+4n3+18n2+52n+75+2n-1(a-150)
(1)
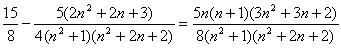
(2)
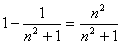
an=2n-7n-13
bn=n3+3n2+9n+13-2n
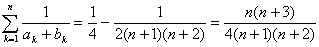
省略(数学的帰納法)
省略
25%
(1) 省略
(2)
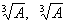
(1) 2
(2) 省略
(3) 省略
(4)
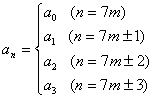
(5) a2=a2-a, a3=a3-3a, a4=a4-4a2+2
(6) x3+x2-2x-1=0
(7)
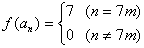
(8) 37/2
(9)
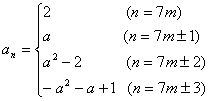
(1) 極大値 q+4 (x=p-2 のとき),極小値 q (x=p のとき)
(2) p=1, q=-2
(3) (p,q)=(2,-4),(-1,-4)
(4) (p,q)=(3,0),(-5/9,0)
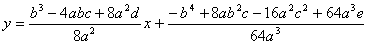
(1) 因数分解 (x-1)2(x3-3x+1)=0
(2) a0=5, a1=2, a2=8,a3=-1, a4=20, a5=-13, a6=59, a7=-61,
a8=188, a9=-244, a10=623, a11=-922, a12=2111
p2q2-4p3r+18pqr-4q3-27r2>0
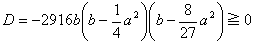 より,
より,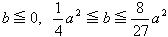
∴
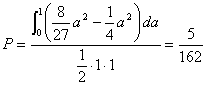
(1) ② → a<-1, 27/5<a, ④ → a<-27/5, 1<a
(2) -1<a<0, 0<a<1
a=xy+yz+zx とおくと
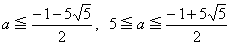
(1) 最大値 2/√3 (x=(2+√3)/3, y=2/3, z=(2-√3)/3)
最小値 1 (x=1, y=1, z=0 または x=4/3, y=1/3, z=1/3)
(2) 2≦x3+y3+z3≦22/9
a=xyzとおく。
最大値 1,最小値 -√3/27
k4=(a4-6a2c+3b2+8ac)/6
k5=(a5-5a3b+5a2c+5bc)/6
(1) 2+3√2, x=π/4
(2)1-2√2
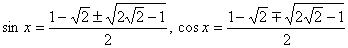 (複号同順)
(複号同順)
13,
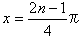
f '(1)/f(1)
省略
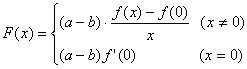
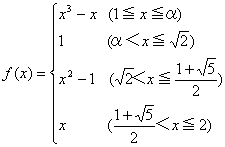
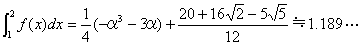
S=(3pβ2+9qβ+2p2)/4
省略
(1)
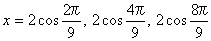
(2)
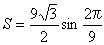
f(x)=xk(a0xn+a1xn-1+a2xn-2+…+an)とおくと,
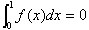 より
より
(1) x=19y/12-7y2/72 (0≦y≦12)
(2) 28
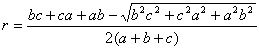
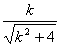
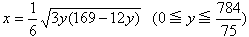 円
円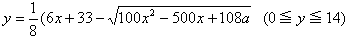 直角双曲線
直角双曲線
(1) 双曲線,2/5
(2) 放物線,1
(3) 楕円,2
(4) 円,4
2abx2-2(a+b)xy+2y2-2abcx+(a+b)cy=0 (双曲線)
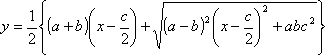
(1) 省略
(2) a=bのとき θ=45°
a≠bのとき
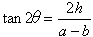
(3) 省略
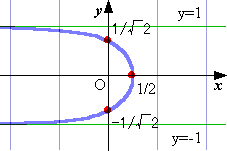
(1) 2x2-2y2+1=0 (直角双曲線)
(2)
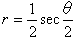
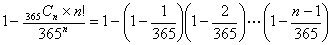
ここでn=20を代入する
=-(364÷365×363÷365×362÷365・・・×346÷365-1)=0.4114383836
と入力すると、オーバーフローなく計算できる。
省略
(1)
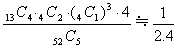
(2)
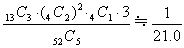
(3)
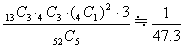
(4)
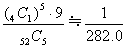
(5)
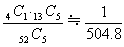
(6)
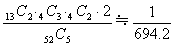
(7)
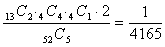
(8)
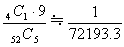
(9)