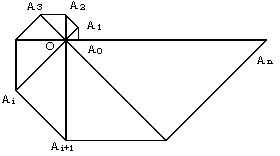
丂丂丂A0(1丆0)丆佢Ai+1OAi=2兾/n丆佢OAiAi+1=兾/2乮i=0,1,2,乧,n-1丆n亞5乯
丂偙偺偲偒丆師偺栤偄偵摎偊傛丏
(1)丂懡妏宍 A0A1A2乧An乮偐偨偮傓傝宍乯偺柺愊傪媮傔傛丏
(2)丂
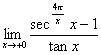 傪媮傔傛丏
傪媮傔傛丏
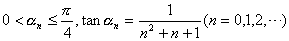 偺偲偒丆師偺栤偄偵摎偊傛丏
偺偲偒丆師偺栤偄偵摎偊傛丏(1)丂tan兛0丆tan(兛0亄兛1)丆tan(兛0亄兛1亄兛2) 偺抣傪媮傔傛丏
(2)丂tan(兛0亄兛1亄乧亄兛n-1) 偺抣傪媮傔傛丏
(3)丂柍尷媺悢
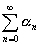 傪媮傔傛丏
傪媮傔傛丏
丂丂丂
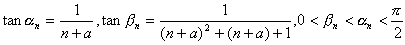
偵傛偭偰掕媊偝傟傞丏偨偩偟丆n=0,1,2,乧 偱丆掕悢 a 偼偡傋偰偺 n 偵懳偟
丂丂丂兛n亅兝n亝3兾/20
傪枮偨偡嵟彫偺惍悢偱偁傞丏偙偺偲偒丆師偺栤偄偵摎偊傛丏
(1) cot 3兾/20 偺抣傪媮傔丆偦偺嬤帡抣傪彫悢戞俀埵傑偱寁嶼偣傛丏
(2) a 偺抣傪媮傔傛丏
(3) tan(兛0亅兛1) 丆tan兝0 丆tan(兛1亅兛2) 丆tan兝1偺抣傪媮傔傛丏
(4) 柍尷媺悢
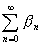 傪媮傔傛丏
傪媮傔傛丏(5) 柍尷媺悢
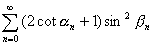 傪媮傔傛丏
傪媮傔傛丏
(1)
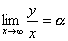
(2)
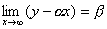
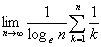 傪媮傔傛丏
傪媮傔傛丏
(1)
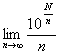 傪媮傔傛丏
傪媮傔傛丏(2)
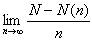 傪媮傔傛丏
傪媮傔傛丏
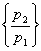 傛傝丆a2=1丆n=3 偺偲偒丆乽p1暘偺p2暘偺p3 乿=
傛傝丆a2=1丆n=3 偺偲偒丆乽p1暘偺p2暘偺p3 乿= 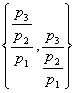 傛傝丆a3=2 偱偁傞丏師偺栤偄偵摎偊傛丏
傛傝丆a3=2 偱偁傞丏師偺栤偄偵摎偊傛丏(1)
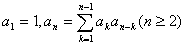 傪徹柧偣傛丏
傪徹柧偣傛丏(2) an傪媮傔傛丏
(3)
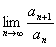 傪媮傔傛丏
傪媮傔傛丏(4)
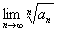 傪媮傔傛丏
傪媮傔傛丏
(1) P(n,m) 傪媮傔傛丏
(2)
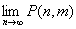 傪媮傔傛丏
傪媮傔傛丏(3) 擟堄偺n 偺抣偵懳偟偰丆P(n,m)亞0.01 偲側傞嵟戝偺 m 偺抣傪媮傔傛丏
丂偨偩偟丆log101.09=0.0374 偲偡傞丏
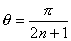 偺偲偒丆
偺偲偒丆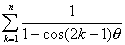 偺抣傪媮傔傛丏
偺抣傪媮傔傛丏
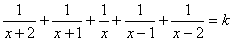 (掕悢)偵偮偄偰丆師偺栤偄偵摎偊傛丏
(掕悢)偵偮偄偰丆師偺栤偄偵摎偊傛丏(1) k亜0 偺偲偒丆惓偺夝俁屄丆晧偺夝俀屄傕偮偙偲傪徹柧偣傛丏
(2) K=0 偺偲偒丆夝傪媮傔傛丏
(1)
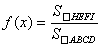 傪媮傔傛丏
傪媮傔傛丏(2) f(x) 偺嵟戝抣偲丆偦偺偲偒偺x偺抣傪媮傔傛丏
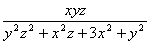 偺嵟戝抣傪媮傔傛丏
偺嵟戝抣傪媮傔傛丏
(1) y=sin x丆y=cos x丆y=tan x
(2) y=cos x丆y=tan x丆y=cot x丆y=sec x
(3) y=cot x丆y=sec x丆y=cesec x
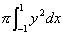 偺抣傪媮傔傛丏
偺抣傪媮傔傛丏
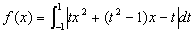 偵偮偄偰丆師偺栤偵摎偊傛丏
偵偮偄偰丆師偺栤偵摎偊傛丏(1) f(-x)=f(x) 傪徹柧偣傛丏
(2) f(x) 傪媮傔傛丏
(3) f(x) 偺嵟彫抣傪媮傔傛丏
(4)
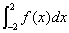 傪媮傔傛丏
傪媮傔傛丏
丂嘆
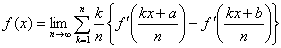
丂嘇 f(0)=0
丂嘊 f '(0)=b-a=c亗0
丂嘋
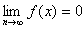
(1) f(x) 偺嵟戝丒嵟彫抣偲丆偦偺偲偒偺 x 偺抣傪媮傔傛丏
(2) 嬋慄 y=f(x) 偲 x幉偲偺娫偺晹暘偺柺愊傪媮傔傛丏
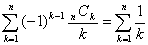 傪徹柧偣傛丏
傪徹柧偣傛丏
(1)
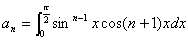 偺偲偒丆
偺偲偒丆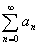 傪媮傔傛丏
傪媮傔傛丏(2)
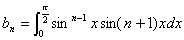 偺偲偒丆
偺偲偒丆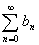 傪媮傔傛丏
傪媮傔傛丏
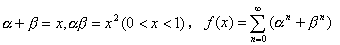 偲偍偔偲偒丆師偺栤偄偵摎偊傛丏
偲偍偔偲偒丆師偺栤偄偵摎偊傛丏(1) f(x) 傪媮傔傛丏
(2) f(x) 偺嵟戝抣偲丆偦偺偲偒偺 x 偺抣傪媮傔傛丏
(3) 嬫娫乵0,1乶偵偍偗傞f(x) 偺暯嬒抣傪媮傔傛丏偨偩偟丆f(0)=2,f(1)=1 偲掕媊偡傞丏
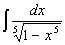 傪媮傔傛丏
傪媮傔傛丏
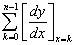 傪媮傔傛丏
傪媮傔傛丏
(1)
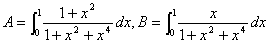
(2)
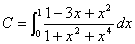
(1) 嘆偑幚悢夝偩偗傪傕偮偲偒丆揰 (a,b) 偺懚嵼偡傞斖埻傪恾帵偣傛丏
(2) k 傪惓偺掕悢偲偟偰丆0亝b/k亝a亝1 傪枮偨偡擟堄偺 a,b 傪慖傫偩偲偒嘆偑幚悢夝偟偐傕偨側偄妋棪 P(k) 傪媮傔傛丏
(3) (2)偱 P(k) 偺嵟戝抣偲丆偦偺偲偒偺 k 偺抣傪媮傔傛丏
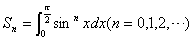 偲偍偔偲偒丆師偺栤偄偵摎偊傛丏
偲偍偔偲偒丆師偺栤偄偵摎偊傛丏(1) 嘆 S0丆S1 偺抣傪媮傔傛丏
丂嘇 Sn丆Sn-2 偺娭學幃傪媮傔傛丏
丂嘊 nSn-1Sn 偺抣傪媮傔傛丏
丂嘋
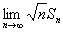 偺抣傪媮傔傛丏
偺抣傪媮傔傛丏(2)嘆 cos x=y 偲偍偔偲丆S2m+1 偼偳偆側傞偐丏
丂嘇 cot x=y 偲偍偔偲丆S2m-2 偼偳偆側傞偐丏
丂嘊 1-y2亝e-y2亝1/(1+y2) 傪徹柧偣傛丏
丂嘋
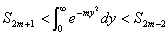 傪徹柧偣傛丏
傪徹柧偣傛丏丂嘍
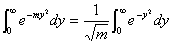 傪徹柧偣傛丏
傪徹柧偣傛丏(3)嘆
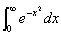 偺抣傪媮傔傛丏
偺抣傪媮傔傛丏丂嘇
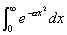 偺抣傪媮傔傛丏
偺抣傪媮傔傛丏丂嘊
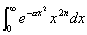 偺抣傪媮傔傛丏
偺抣傪媮傔傛丏丂嘋
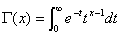 偲偍偔偲偒丆
偲偍偔偲偒丆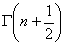 偺抣傪媮傔傛丏
偺抣傪媮傔傛丏