1　はじめに

1.1　作図（折り方）の基本

1. 線分の垂直二等分線(２点A、Bを合わせて折る）[図(a)]
2. 角の二等分線(線分AB、APを合わせて折る）[図(b)]
3. 任意の点から線分に垂線を引く（折り線が点Pを通るように点Aを線分ABのせて折る）[図(c)]
4. ２点を通る直線を引く（2点P,Qを摘まんで折る）[図(d)]

1.2　三角形の角の二等分線と比

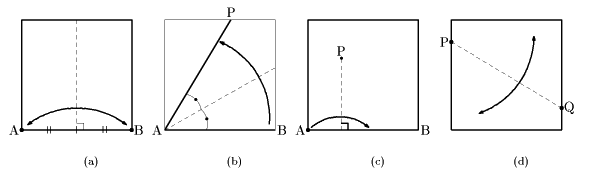
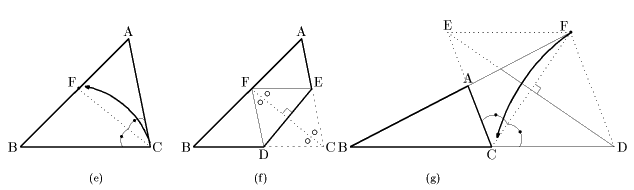
三角形ABCの頂角∠Cまたはその外角の二等分線AF(折り紙的証明)

　2等分線CFを折り、次に頂点Cが点Fに重なるように折ります。[図(e)]（外角についても同様）
　すると、図(f),(g)　において、四角形CDFEは菱形になり、FE//BC,FD?//AC$であることが分かります。
　また、このことから△AFE∽△FBD∽△{ABC}であり、FE=FDに注意すると
　　　AF:FB=FE:BD=FD:BD=AC:BC　　ただし、図(g)ではAC≠BC

1.3　対称移動

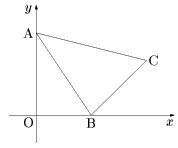入試問題より(1) x-y平面上の3点A(0,3),B(2,0),C(4,2) を頂点とする三角形（右図参照）について、次の(1),(2) に答えよ。 ある直線に沿ってこの三角形を2つに折ったところ、点Cが点Aにぴたりと重なった（点Aは動かないように折った）。このとき、 この直線の方程式を求めよ。 このとき、点Bが移った点の座標を求めよ。 神戸女子大　2001

　折ったときに重なる2点A,C は、この直線を折り目として線対称である。

原点を通る直線lに関する対称移動

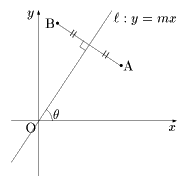　原点を通り、x軸の正の向きとなす角がθである直線に関する対称移動はA(x,y),B(x',y') として
　　　
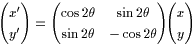
であり、m=tanθとすると
　　　
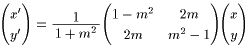
と表される。
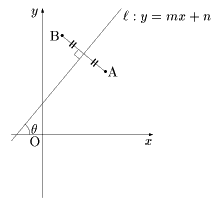y=mx+nで表される直線lに関する対称移動

　　　
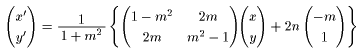
と表される。