【付録】

続・多角形をたたむ

（外心で遊ぼう）

　前回のレポートでは「多角形はすべての辺だけが一直線上に重なるように折りたたむことができる」ことを取り上げました。

　今回はその続編です。

　前回のレポートについて、簡単な場合を授業でも取り上げてみました。が、授業として成立させるためには、問題提示と発展性について何か具体的なものの必要性を感じました。また、授業の中で一人の生徒が行った行為がヒントになって、食塩で内心・傍心を求める実験が可能であることが分かりました。(付録参照）

　ところが、その後新学期に入り、黒田俊郎さんという方がすでに「平面幾何のは・な・し」（三省堂：1999.10刊）いう本の中でこの実験を書かれていることが分かりました。「食塩は炭酸カルシウム入りのものが湿気を吸わずサラサラとしているのでおすすめ・・・」という気配りもされています\footnote{小４から高校以上までをスローガンに、工作用紙もつけ細かい配慮がされた本です}。最後の「追伸のページ」の中で「内心・外心を食塩で求める」ことが具体的に書かれています。さらに、「垂直二等分線」の説明の中で「3つ以上の小学校があったら、校区はどのようにきまるでしょうか？」と問題を提起されています。

　そして、幸運にも黒田先生のレポート（１９９８．８付け）を数教協の全国研究会に参加された先生からいただくことができました。それをみると「砂が教える内心・外心」の中でも次のように問題提起をされています。

『右のような島がある。「最も近い海岸に行く」というルールで、「行くべき海水浴場」を決めるとすると、どういうふうに区割りができるか？このアルゴリズムは？
右のような図を書けばよい。（これは等高線ではないか？）

　砂山をつくれば、自然に「行くべき海水浴場」が決まるのではないか？』

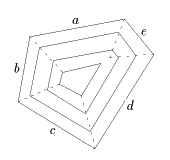
これが、先にあげた本の内容に結びついているようです。（この等高線、授業で一人の生徒が折りたたんだ多角形を下辺に平行に短冊状にはさみで切り、広げた行為そのものでした） 　前回の私のレポートは、この砂山（塩山？）の作る稜線を求めることでもあったわけです。（右図）（ただし、凸多角形の場合であり、そうでない場合は一部放物線で補正しなければなりません）もちろん定規とコンパスで作図もできます。 　すべての辺を1直線上に揃えてたたむ手順そのものが区割り法のアルゴリズムです。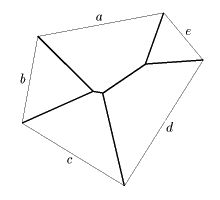

　以上は、内心・傍心に関するものですが、黒田先生は今回のテーマである「幾何学的最短距離通学区域決定法」にもレポートで触れられ、「学区を決定するアルゴリズムは？」と書かれています。（本では食塩で外心を求める方法を工夫されています。）

　この問題を考えてみることにします。この「幾何学的最短距離通学区域決定法」という言葉は「型破りの数学」^(注)（1976.3刊）という本の中で「小説的数学試験問題」として書かれています。解説の中で、アルゴリズムは述べられていませんが「７校までやってみた」とあります。そこで、私も７校でやってみることにします。

(注)吉田賢憲著：著者は当時中学校教諭で、この問題は中学3年生用のテスト問題として作成されたようです。著者の好きな言葉:「数学が他の学問と違う点は、伝統や経験にとらわれないで、自由に考えることのできる点にある」−ＧＥＯＲＧ・ＣＡＮＴＯＲ

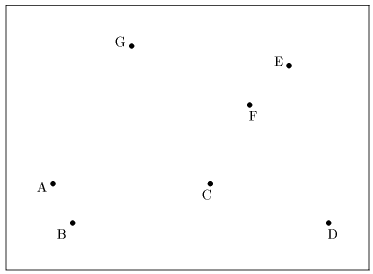
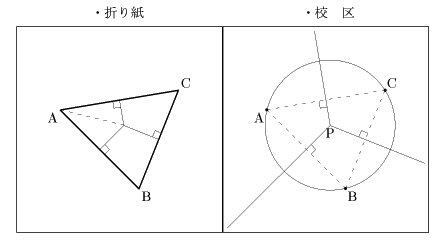
　この問題の解答の前に、「多角形はすべての頂点が重なるように折りたたむことができる」ことを三角形、四角形で確かめ、それに対応して学校数が３、４校の場合の校区を決定してみましょう。（多角形の折りたたみ方の詳細や3校が1直線上に並ぶなど特殊な場合については、省略します）

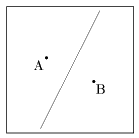メモ１　学校数が2校のとき

• 学区の境界は線分ABの垂直二等分線
• 折り紙では2点A,Bを重ねて折る

• △ABCにおいて、辺AB,ACの垂直2等分線を折り（山折り）、交点と頂点を結ぶ線を谷折りにして包むように折ると第３の垂線（辺BCへの）が自然にでき、３頂点A,B,Cは重なる。
• Pは△ABCの外心

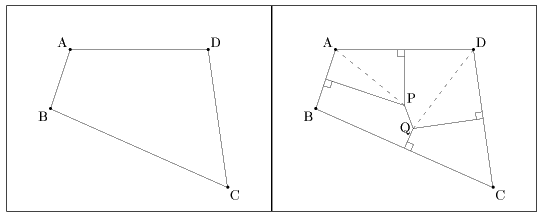
メモ３　学校数が4校のとき

• 四角形ABCDの４つの辺の垂直2等分線を折り（山折り）、隣り合う２辺の垂直2等分線の交点のうち、最初に交わる点Pをとり、APを谷折りにして３頂点A,B,Dが重なるようにたたむと第３の直線が折れ、辺BC、DCの垂直２等分線の交点Qと交わる。次にQDを谷折りにしてたたむと、頂点Cは３頂点A,B,Dに重なる。
• この山折り線が校区の境界線となる
• 点Pは△ABD,点Qは△BCDの外心です。

メモ４　なぜ２点P,Qなのか。

• 3頂点の組合せは他にも存在しますが、仮に下図右のように△ABCの外心Rを選んだとすると、頂点Dはこの外接円の内部に存在し、３頂点A,B,Cよりも近い距離にあることになり、条件に反します。当然このRを頂点としてたたむと、頂点Dは他の頂点に重ねることはできません。
• メモ３の「隣り合う２辺の垂直2等分線の交点のうち、最初に交わる点」はこのことからきています。したがって、作図的には外接円の内部に３頂点以外の点が存在しないことが条件となります。（厳密にはこれだけでは正確ではないようです。）

• こうして、下図のように校区が決まります。

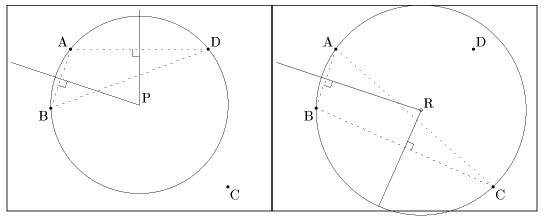
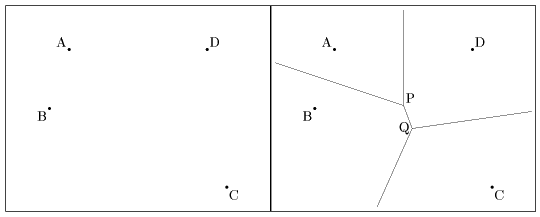
メモ５　学校をもう１校新設した場合、校区はどう変わるか。

• 下図の白丸の場所に学校を新設すると、点Bと白丸の垂直２等分線を引き、境界線とぶつかったところで今度は点Aとの垂直２等分線を引く。これを繰り返し一回りしてもとにもどる。この線で囲まれた領域が新設校の校区となる。
• 折り紙では、下図のように切り取り、各頂点をBから順に次々と白丸に重なるように折りたたむとよい。
• 基本的にはこの操作を次々と行うことによって、学校数がいくつであっても校区を決定することができる。

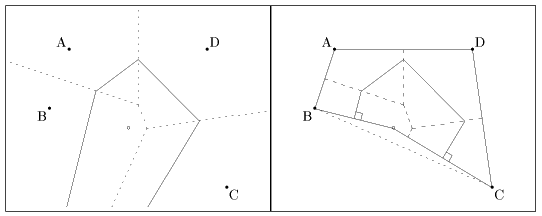
解答　以下の通り。

• 下図のように７角形を左下から折り始めて７頂点が重なるように折り、開いてできた折り線で校区を決定することができる。

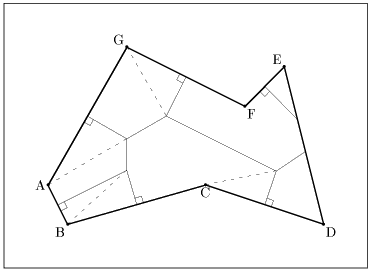
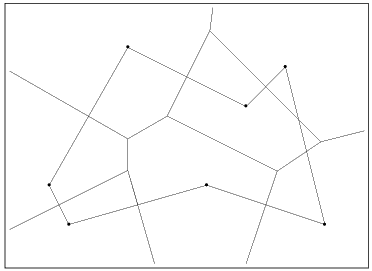
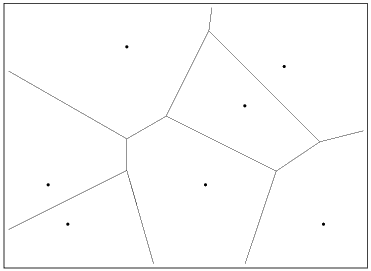
メモ６　このレポートをまとめはじめた頃、数学セミナー５月号に「コンビ二を開店するのに有利な場所は？」という一文が掲載された。調べてみると過去にも数学セミナー（１９９６．４〜１９９７．３）に「ボロノイ図を通してみると…　杉原厚吉」が連載されていました。

　生物のなわばりや結晶構造などの自然現象から、施設の配置問題、ロボットの制御など工学的応用まで多様な関わりがあるそうで興味深い。高校における、内心、傍心、外心の指導の発展方向の一つ（なわばりの幾何学等と称して）として教材化が可能ではないだろうか。

【付録】