 �������B
�������B���̌��ʁA�T�̉Ƃ��āw�`�a���n��rank�`�{rank�a�����x��������B�@����
| (�R) �T�@�`�a���n�ƂȂ�`�C�a�̕K�v�\�������͉����H |
�`���i���C���j�C�a���i���C���j�Ƃ���B
Prop�Q �`�a���n�̂h���a��Ker�`
Cor�@�@�`�a���n��rank�`�{rank�a����
 �����藧�Ƃ͌���Ȃ��B�����ŁA����q�����߂Ē�`����B
�����藧�Ƃ͌���Ȃ��B�����ŁA����q�����߂Ē�`����B
Def�W�i����q�̒�`�j
�@�`������q�Ƃ́A�n�łȂ��`�ɑ��āA�a���n ��.��. �`�a���n �܂��� �a�`���n
�@���̂悤�ɒ�`���āA�wrank�`�{rank�a�����x�����肷��ƁA�`�ɑ��āw�h���a��Ker�`�x�܂�a��(��'�P�c��'��)��Ker�`��{���P�c����}����sub.sp.�ƂƂ�ACor�� �������B
�������B
���̌��ʁA�T�̉Ƃ��āw�`�a���n��rank�`�{rank�a�����x��������B�@����
| �S �C�ӂ̍s��`�ɑ��āA�`�a���n�C�b�`���n�ƂȂ�a�C�b�����ꂼ��\������B |
�`�a���n�ƂȂ�a�̍\���ɂ��ẮA�R�Ŗ��炩�ɂȂ����B
���ɁA�b�`���n�ƂȂ�b�̍\���ɂ��ẮC�b���i���C���j�s��Ƃ���Ɓ������A�w�b�`���n��rank�b�{rank�`�����x��������B
��̓I�ɂ́CProp�P���g���ƁA�u����Im�`�Fsub.sp.���A�u����(Im�`) (Im�`)��
(Im�`)��
(Im�`)���߁o�����u���F���S��'�����O�C�P���͂������p���o�������u���Ft���`���O�p
�@�����ŁA�s�x�N�g���Ft�����i��1�c�����j���u���͂u����sub.sp.�ł���B����āA
�@�@�@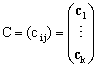 �@�@�������u��
�@�@�������u��
�P���͂������̍\���́A�`�ɑ��āA�o���P�c�����p��(Im�`)����sub.sp.�ƂƂ�悢�B
�@�ȏ�̒��ŁA�wDef�W�i����q�̒�`�j�x������A�����A�⑫���܂��B���̒��́A�����͐������܂���B���̂Ȃ�A�wrank�`�{rank�a�����x�����肷��ƁA���̂Ƃ��`�C�a�́A���ɗ^�����Ă���̂ŁA�`�ɑ��āw�h���a��Ker�`�x�A�܂�a��(��'�P�c��'��)��Ker�`��{���P�c����}����sub.sp.�ƂƂ邱�Ƃ͂ł��Ȃ�����ł��B
�@���������āA����ɊW�����������A���L�̒ʂ�ɒ������܂��B
�@�܂��A���̒����̒��ŁA������q�A�E����q���g���Ă��܂��̂ŁA��L��Def�W�i����q�̒�`�j�w�`������q�Ƃ́A�n�łȂ��`�ɑ��āA�a���n ��.��. �`�a���n �܂��� �a�`���n�x���A�{�e�V�ł�Def�P�ŁA������q�A�E����q�A������q�܂Ō��y���čĒ�`���܂����B
�m������n
�@��LProp�Q��Cor�̋t�́A���藧���Ȃ��B
�@�{�e�V�ł�Def�P�̂悤�ɒ�`����ƁA�U�̉́A�^����ꂽ�`�ɑ���Prop�Q���A�w�h���a��Ker�`�x�A�܂�a��(��'�P�c��'��)��Ker�`��{���P�c����}����sub.sp.�ƂȂ�悤�ɂa���\������悢�B�a���n�͎����ł���̂ŁA��������O�����a���\���ł��邽�߂̂`�̏������l����ƁA���̂悤�ɂȂ�B
Prop�R �`��������q�̂P��rank�`�����|�P
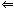 �jTh�R��Cor���A�P�����|dim(Ker�`)�����|�P ���P��dim(Ker�`)�����|�P
�jTh�R��Cor���A�P�����|dim(Ker�`)�����|�P ���P��dim(Ker�`)�����|�PCor�P �`���E����q�̂P��rank�`�����|�P
Cor�Q �`������q �̂P��rank�`��Max(���C��)�|�P
�@���ɁA�b�`���n�ƂȂ�b�̍\���ɂ��ẮC�b���i���C���j�s��Ƃ���ƁCProp�P���A
�@�@�@�u����Im�`�Fsub.sp.�A�u����(Im�`)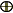 (Im�`)��
(Im�`)��
�@(Im�`)���߁o�����u���F�����'�����O�C�P���͂������p
�@�@�@�@�@���o�������i���P�c�����j���u���F�����`���O�p
�͂u����sub.sp.�ł���B
�����
�@�@�@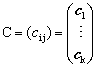 �@�@�������u��
�@�@�������u��
�P���͂������̍\���́A�`�ɑ��āA�o���P�c�����p��(Im�`)����sub.sp.�ƂƂ�悢�B
�m�ȏ�A�����I�n
�@�{�e�́A�O��ƃ����N���Ă���̂ł����A�O��̃��|�[�g���݂Ă��Ȃ������ΏۂɋL�q���܂����B���̂��߁A�O��ƈꕔ�d�����Ă���Ƃ��낪����܂��B
�Q���̐����s��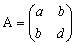 �ɂ��ẮACaylay-Hamilton�̕����� �`�Q�|(���{��)�`�{(�����|����)�d���n���g���A�`�̂����������e(�`)���n�ɑ��Ă`�̎����������āA���`�����d�Ƃł���B �ɂ��ẮACaylay-Hamilton�̕����� �`�Q�|(���{��)�`�{(�����|����)�d���n���g���A�`�̂����������e(�`)���n�ɑ��Ă`�̎����������āA���`�����d�Ƃł���B�i�@�js���O�̂Ƃ��A�`�����d�C�����ł��͂e(��)���n�̉� �i�A�js���O�̂Ƃ��A�����O�C���̂Ƃ��`�́A���������O�Ȃ�s�� �Ƃ��Ă���B |
�@���̕��@�����Ɂw���`�����d�@�x�Ɩ��t���悤�B
�@�Ƃ��낪�A�����́w���T ������ ���A�x�ŁA�w(�`�|�Q�d)(�`�{�d)���n���Adet(�`�|�Q�d)���O�Cdet(�`�{�d)���O����A�`���Q�d�C�|�d�ȊO�̉��邱�Ƃ��ł��邪���_�I�ɓ�_�����邱�Ƃɒ��ӂ��Ȃ���Ȃ�Ȃ��x�Ƃ��Ă���B
�@�����̂����ł�����_�Ƃ́A����q�̑��݂ł���B�܂�A�s��������������ɓ�����A�����͂�����̂�����q�Ȃ̂ł���B
�@���ۂ̋���̌���ŁA���k�Ɏw������ꍇ�́A��L�́w���`�����d�@�x���e�Ղł���A����q������Ďw�����邱�ƂɂȂ�B�������A���k�͌�q�̂悤�ɗ���q�ɋ����A�S�������Ă���̂ŁA����I�w���̗��ꂩ��́A�t�ɐϋɓI�ɗ���q�����������@�Â��ɑ傢�Ɋ��p���������̂ł���B�������邱�Ƃɂ���āA���t���g�����k�Ƌ��Ɋw�Ȃ��琔�w�̐��E���L�����悤�B
�@�{�e�̖ړI�́A�O��̃��|�[�g�W�����A�w�s��ɂ��������q�Ƃ͂����Ȃ�\�������Ă��邩�x�Ƃ������k����̎���ɁA����ɋ�̓I�ɉ�����Ƌ��ɁA����q�����p�����s��������̉�@�ł���B
�@�{�e�ł̃L�[���[�h�́A������q�ł��邪�A���̃A�C�f�A�́A�ɂ߂ĒP���ł���B����́A(�`�|�Q�d)(�`�{�d)��(�`�{�d)(�`�|�Q�d)���n���ώ@���Ă��āA�`�|�Q�d�Ƃ`�{�d�Ƃ����ł��邱�Ƃ���v�������̂ł���B���������āA�{�e�́A���́w������q�x���d�v�ȏ����Ƃ��ēW�J���Ă���B
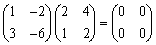 �@�@
�@�@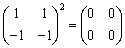
(�P)�@���Z���ɂƂ��Ă̗���q
�@���Z���ɂƂ��ď��߂Ă̗���q�Ƃ̏o��́A�V�N�ȋ����ł���B�{�Z�ł��A���Đ��w�b�̎��ƂŐ��k����w�s��ɂ��������q�Ƃ͂����Ȃ�\�������Ă��邩�x�w�ǂ�����Η���q�������̂��x�Ƃ������₪����������łȂ��A��N�̖{�Z���k�̉���J�p���N�́A�ȉ��̒ʂ�̏����������݂��B
(�Q)�@���k�̏������i�v�|�j
�@��L�̂悤�ȗႩ��A�Q���̐����s��ɂ��āw����q�ˋt�s��������Ȃ��x���Ƃ��\�z�����̂ŁA�����w���@�ɂ���ďؖ��B�i�K�v�����j
 �@�Ƃ��낪�A�t��
�@�Ƃ��낪�A�t��
�@�@�@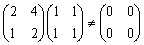
�̂悤�ɁA�w�t�s��������Ȃ��x����Ƃ����āw����q�x�ɂȂ�Ƃ͌���Ȃ��̂ŁA�\�������ɂ��Ă��l�����B
�@�@�@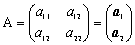 �@�@
�@�@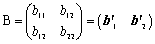
�Ƃ����Ƃ��A�K�v�������A���P//���Q�A��'�P//��'�Q�ł��邪�A�K�v�\�������Ƃ���
�@�@�@ �w�`�a���n���������'�����O����������'���@�P���͂��C�����Q�x
�����B
Def�P�i����q�̒�`�j
�@ �`��������q�Ƃ́A�n�łȂ��`�ɑ��� �a���n ���D���D�`�a���n
�A �`���E����q�Ƃ́A�n�łȂ��`�ɑ��� �a���n ���D���D�a�`���n
�B �`������q�Ƃ́A�`��������q�܂��͉E����q�A�܂�
�@�@�n�łȂ��`�ɑ��� �a���n ���D���D�`�a���n �܂��� �a�`���n
�C �`��������q�Ƃ́A�`��������q���E����q�A�܂�
�@�@�n�łȂ��`�ɑ��� �a���n ���D���D�`�a���a�`���n
Remark ���̂悤�ɒ�`����ƁA�w�o������q�̂o�͋t�s��������Ȃ��x����������
Def�Q�i�s�����A���j
�����s��o�C�p�ɂ���
�o�Ƃp���w�s�����x�Ƃ́A�o�Ƃp�̑Ή�����e�s�x�N�g�����m���]��
�o�Ƃp���w���x�Ƃ́A�o�Ƃp�̑Ή�����e��x�N�g�����m���]��
Remark �ʏ�̐��^�㐔�w�ł�
�@�w�o�Ƃp�����́` s.t. det�`���O ���� �p���`-1�o�`�x�ƒ�`���Ă��邪�A�����ł̍s�����A���Ƃ́A�P���Ɋe�s���̐����̒萔�{�̂��Ƃł���B
�ȉ����ׂāA�Q���̐����s��Ɍ�����̂Ƃ���B
Lemma�P�i������q���m�܂��͉E����q���m�̊W�j �`���O�̂Ƃ��A
�@�@�a�`���b�`���n�˂a�Ƃb�́A�s�����A�܂�A������q���m�͍s����
�@�@�`�a���`�b���n�˂a�Ƃb�́A���A�܂�A�E����q���m�͗�
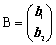 �@
�@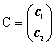 �Ƃ����Ƥ�a�`���b�`���n����������'�����������'�����O
�Ƃ����Ƥ�a�`���b�`���n����������'�����������'�����O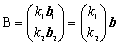 �Adet�b���O���
�Adet�b���O���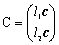 �Ƃ����ƁALemma�P���a�Ƃb�͍s�������������������Ƃ�����
�Ƃ����ƁALemma�P���a�Ƃb�͍s�������������������Ƃ�����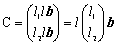
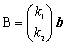 �Ƃb�͗����A
�Ƃb�͗����A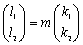 �Ƃ����Ƃb��(����)�a�������B
�Ƃ����Ƃb��(����)�a�������B
 �ɂ��ẮA�w���@�ɂ�萬��
�ɂ��ẮA�w���@�ɂ�萬��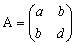 �Ƃ���ƁAdet�`�������|�������O
�Ƃ���ƁAdet�`�������|�������O
�m��P�i�n�a�̑��݂�����
Caylay-Hamilton�̕��������A�`�Q�|�i���{���j�`���n
�@�@�@{�`�|(���{��)�d}�`���`{�`�|(���{��)�d}���n
����āA�`���n�ɑ��āA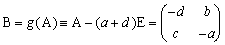 �Ƃ����A
�Ƃ����A
�a���n ���� �a�`���`�a���n ����������
�m��Q�i�n�a�̈�Ӑ�������
if�C�b���n s.t. �`�b���b�`���n�Ƃ����
det�`���O�A�a�`���b�`���n ���� �`�a���`�b���n���������Ă���̂ŁA
Lemma�Q.���C�����O:�X�J���[ s.t. �b�����a
����āA�b�͂a�̒萔�{ �ƂȂ�A�a�̈�Ӑ�����������@�@��
Th�Q.�i������q�̍\���j
�`���n�A�a���n�Ƃ���B�`��(��ij)�C�a��(��ij)�ŕ\����
�@�@�`�a���a�`���n��det�`��det�a���O ���� �����O:�X�J���[ s.t.
�@�@�@�@�@�@�@�@�@�@�@����ii�{��jj���O�C����ij����ij�C�P���͂��������Q
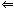 �ɂ���
�ɂ���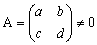 �Ƃ����ƁAdet�`�������|�������O
�Ƃ����ƁAdet�`�������|�������O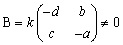 �ƂȂ�
�ƂȂ�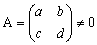 �Ƃ���ƁAMain Theorem�P�D���
�Ƃ���ƁAMain Theorem�P�D��� �ł��邩��
�ł��邩���@�p��s��́ADef�P���������q�̓��ʂȏꍇ�ł���B����Cor�Q.�悤�ɁA�s����������d���̂Ƃ��A�p��s��ɂȂ�̂ŁA�p��s��̍\���ɂ��Ă����ׂ�K�v������B
Pop�P�D�i�p��s��ƌŗL�l�j �@�`��p��s��A�܂�`�����n ���� �`���|�P���n�̂`�̌ŗL�l�͂��ׂĂO
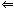 �ɂ��ẮACaylay-Hamilton�̕������ʼn��ƌW���̊W���琬��
�ɂ��ẮACaylay-Hamilton�̕������ʼn��ƌW���̊W���琬��Cor�P�D�Q���̐����s��ł́A�`���p��s��� �`�Q���n ���� �`���n
Remark�Q�D����Cor�̌��ʁA�p��s��`�̍\���́A�����Q�̂Ƃ��ɂ��Ē��ׂ�悢
Cor�Q�D(�`�|���d)�����n,�����Q �� �`�����d�A���d�{�`�O ������ det�`�O��tr�`�O���O
 �Ƃ����ƁA
�Ƃ����ƁA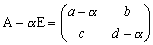 �@
�@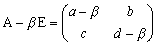
�@Th�Q�́A�w������q�̍\���x�ɂ��Ă̖����Ȍ��ʂł���B������\�ɂ����̂́AMainTheorem�P�Łw������q�̉��̑��݂ƈ�Ӑ��x���ۏ��ꂽ����ł���B��ʂɁA���w�ł́A���݂͗e�Ղł��邪�A���̈�Ӑ������ɂȂ邱�Ƃ������B
�@��̗���グ��ƁA�Ⴆ�Ζ{�Z�̐E�����N���F�[�V�����ł��āA�]���I�ɏo�肳�ꂽ���ł���B�w�P�^�R��(�P�^��)�{(�P�^��)�{(�P�^��) ���݂����قȂ鎩�R���i���C���C���j�̑g���R�O�b�Ԃŋ��߂�x�ƌ����Ď��ԓ��ɂł��Ȃ��������Ƃ�����B�v�̂̂����l�́A�������C���C���Ƃ��ēK���ȂR�̔{�����l���āA�����Ă�����ł��낤�B�������A���̌��ʁA�����̂P�����o���ꂽ�Ƃ��Ă��A����͓����̂P�����܂��������ł����āA���̑S�Ăł���ۏ͂Ȃ��B�������A�Z���Ɛ��w�̕���_�ł���B���w�ł́A���̑��݂̎��ɁA���͗B����A����ȊO�ɉ��͂Ȃ����A����ɘ_���Ȃ���Ȃ�Ȃ��̂ł���B
�@�{�e�ŁA�Q���̐����s��ɂ��āA�w������q�̍\���x�����炩�ɂȂ������A������R���ȏ�ɂ���Ɨl������ς���B�R������Ԃ��l���������ł��A�`�a���n�̂Ƃ��A���̂悤�ɂR�ʂ�l������̂ŁA��Ӑ��͌����Ȃ��Ȃ��Ă��܂�����ł���B
�`�C�a���R���̐����s��̂Ƃ�
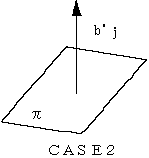 �b�`�r�d�P�F�`�C�a���Q���̂Ƃ��̒P���Ȋg���B���̂Ƃ��A��i�A��'j�łP�̕��ʃ����肵�Ă���B�i���R������Ԃ̐^������ԂƂ����B�j
�b�`�r�d�P�F�`�C�a���Q���̂Ƃ��̒P���Ȋg���B���̂Ƃ��A��i�A��'j�łP�̕��ʃ����肵�Ă���B�i���R������Ԃ̐^������ԂƂ����B�j
�b�`�r�d�Q�F��i���P�̕��ʃ����肵�āA����'j �i���̂Ƃ��A���o��'j�p�̒�����ԁA�܂��́o��'j�p���̒�����ԂƂ����B�j
�b�`�r�d�R�F��Ƌt����'j���P�̕��ʃ����肵�āA����i�i������Ԃ����l�j
�܂Ƃ߂�ƁA��ԁi�R�����j�ł�
�w�`�a���n����i���܂ޕ��ʃ܂��͒������ƁA��'j���܂ޒ������܂��͕��ʃ����A�����x
�@�@(���̂Ƃ��A���ʃA���������A���ꂼ�꒼�����A���ʃ��̒�����ԂƂ����)
�@��ʂɁA������������Ɋg������ƁA��������Ԃ𐂒��ȂQ�̕�����Ԃv�P�A�v�Q�ɕ��������Ƃ��A���̂v�P������i���A�v�Q������'j���Ƃ�A�`�a���n����������B
�@���̂悤�Ɉ�Ӑ��͖����Ƃ��Ă��A�O��̃��|�[�g�ł�������Ԃʼn�����q�̑��݂��ؖ��ł����̂ŁA���������s��̒��ʼn�����q���W���I�ɂǂ�Ȉʒu�t���ɂȂ邩��������]�n�͎c���Ă���B���̏ꍇ�A�{�e�ł̋c�_���ǂꂾ���R�����ȏ�Ɋg���A���W�ł��邩�A���̂Ƃ���S�����ʂ��Ă��Ȃ��B�܂��A�Q�������s��ł��A�s�������̉�@�ȊO�ɁA������q�����p���l������B
�@����I�ɂ������I�ɂ��A����q�͂��̒�`����B���ŁA���҈�������Ă���悤�Ŏc�O�Ȃ��Ƃł���B��ʂ̗���q�́A���炩�Ɍ����Ώۂɂ͂Ȃ蓾�Ȃ����A�s��ɂ��������q�͑傢�ɋ���I�������I�ɊJ���̗]�n���c���Ă���Ǝv���B
(�Q)�@���w����ɂ���������ӔC
�@�ŋ߁A�����J�Ƌ��ɐ����ӔC������Ɍ�����悤�ɂȂ����B���w����̐��E�ł��A���낢��ȏ�ʂŐ����ӔC�������ł��낤�B���̒��ŁA���k����̐��w�Ɋւ��鎿��A�^��ɑ��āA������ƑΉ����邱�Ƃ́A�����ӔC�Ƃ������Ƃ��g���܂ł��Ȃ��A���w���t�Ƃ��Ă͓��R�̋`���ł���B�����̐ӔC��`�����ʂ����Ȃ��ƁA���t�Ɛ��k�Ԃ̐M���W�͍��{�������Ă��܂��ł��낤�B���w���t�Ƃ��Đ��w�Ɋւ��Đ��k�ɐӔC�������߂ɂ́A����́w����q�x�Ɍ��炸�A��b�����͕K�v�s���ł���B