１　学校概要

　大正１１年の創立以来、秩序と調和を持って空知の高等学校教育を推進してきた伝統校である。入学者のほとんどが明確な進学希望を持っており、全道有数の進学校として知られている。

２　エンカウンターの目的

　エンカウンターとは「心とこころの交流」とか「ホンネとホンネの交流」と解釈される、裏表のない人間関係のことである。自分の心を開き、他者との関わりの中で自己の存在や個性に気付き、意欲的な人間へと変容させる。―そういう体験を意図的にしようというものである。
　では具体的にどんなことをするのか。リーダー役の人間が次々と作業・ゲーム・討議といった課題（エクササイズ）を与えていき、その体験を通し、胸襟を開いた感情交流をしようというものである。
　つまり教師が教授するのではなく、生徒同士が教育しあう場面だと思えばよい。
　エンカウンターには一対一のものとグループのもの、構成法と非構成法などいくつかの種類があるが、ここで取り扱うのは構成的グループ・エンカウンターである。
　では、なぜエンカウンターなのか。その必要性は何かというと、４つある。
　一つは、世の中の変化の進度が以前よりは激しくなってきたため。
　つまり、変化の激しい時代にあっては、周りから指示や命令を待つのではなく、自ら主体的に他者との関わりを持たなくては、結局誰とも交流できぬまま孤独感にとりつかれてしまう。
　「やあやあ。ボクは○○な人間です」と自分を開き、自分を理解してもらう能力が必要となってくる。他者との関わりにおいて、自己の個性を知り、他者への理解も生まれる。
　これは、クラス替え、転学、進学といった生徒の文化においても同じである。
　二つ目は世の中の構造が組織化し、以前よりも「他と共に」ということが求められるようになったため。
　「我関せず」式では、組織の中では生きにくいし、感情交流がもてない。感情交流がもてないということは、感情の処理が難しいということになる。したがって心が癒せず、ストレスがたまるという結果になる。
　ゆえに、人間関係の持ち方の技法が必要となり、グループ・エンカウンターによりリレーション体験の場を設定しようというものである。
　三つ目は個の自覚ということ。これは簡単に云うとアイデンティティーの確立ということである。他との関係における自己を意識した上で、「自分はこう生きる」という気概を打ち出さねばならない。他者を理解した結果、仲間意識を持ち、そのグループに同一化しすぎて、個としての自分を見失ってしまうのでは意味がない。
　人と同じようになろうと願う自分と、唯我独尊という自分がやはり適度に行き来することが、望ましい人格形成だと思う。
　第四の理由は世の中の現実原則を理解するということ。
　人間が成長するということは、幼児的・自己中心的な依存性から大人の相互依存へと人間関係が変化することである。
　相互依存とはギブ・アンド・テイクの関係である。
　テイクされるばかりでギブしない人は我が儘と見られるし、かといってテイクを受け入れないのも「可愛げのない人」と見られる。
　赤ん坊ですら母親の愛を獲得するために笑顔をギブしている。
　お互いにギブ・アンド・テイクすることが他と共に生きて学ぶことであり、そのために他者に自分のなし得ることをすればよい。
　以上を要約すると、エンカウンターは自分自身がなんたるかを知らしめる。他者との関係の中に生きる自分に気付かせる。他を信頼しつつ自己を実現していく意欲的な人間に変身させる。
　これこそ望ましい学校・学級集団の一員として教師が求めてやまない生徒像だと云える。

３　エクササイズについて

　エンカウンターを展開する上での柱が二本ある。
　エクササイズとシェアリングである。
　エクササイズとは、教師の考えるねらいを達成するために用意された課題のことである。生徒は、教師の用意したエクササイズを行うことによって、授業のねらいを達成していく。
　また持ち時間や参加者、会の目的に応じてこれらのエクササイズの内容や配列順序は違ってくる。
　このエクササイズを行いながら授業は展開されていく。
　また、エクササイズはカウンセリングの様々な理論によって構成されているので、ねらいの達成方法が明確に示されているし、どの程度達成されているのかも知ることができる。
　もう一つの柱であるシェアリングとは、分かちあいや振り返りのことである。エクササイズを振り返ることによって、そこでの気づきや感情を明確化し、ねらいを定着させる働きをもっている。
　さて、今回の授業で行ったエクササイズは後掲の指導案にある七つである。
　この七つのエクササイズを導入として、三角関数のグラフについてのグループ学習へと展開させていった。
　そこで七つのエクササイズの意味づけを考えてみたい。

1. 三人の人間と握手する
   　ウォーミングアップである。メンバーである生徒同士のリレーションがはかられると、後の考察も短時間で深まったものになる度合いが少なくない。

2. フロア内を自由に歩き、握手する
   　このエクササイズの最中に何度かストップをかけ、ねらいを伝えた。
   　人の後ろについて同方向にぐるぐる歩く生徒がいる。「人の後に続く方が安定への欲求が満たされるからだが、一人で自由に歩いてほしい。フロア内を歩くくらいの自由は自身で獲得してほしい。そのための孤独、不安に耐えられないようでは、人に頼られる人間になれない」と叱咤激励。
   　相手の目を見ないで握手する生徒がいる。「目は感情表現のチャンネルである。目で挨拶しながら握手をしてほしい。これからの国際社会に、握手くらいできなくてどうするのか」と注意を促す。
   　このエクササイズを続ける中で、他者に握手を求めていく積極的な生徒と握手されるのを待っている受け身的な生徒がいることに気付く。
   そこで再びストップをかけ、「自らアクションを起こせ、受け身的ではいけない」と注意した。

3. 二人一組（相互質問）
   　相手について知りたいことを聞く、というこのエクササイズは、「私はあなたに関心がある」ということを伝えるエクササイズである。
   　聞かれる方は、この人はこれほど私に関心を持っているのかと嬉しい気持ちになる。
   　心とこころのふれあい（エンカウンター）は、お互いに関心を持ちあうことからスタートする。
   　ペアを組む相手はフロア内を握手しているときにストップをかける。そのときの相手とペアになるので必ずしも親しい間柄ではない。
   　このエクササイズから教室内は急ににぎにぎしくなる。多くのペアが同時に会話をするからである。しかしこれは好ましい現象と云える。表情や身振り手振りを見ていると、それぞれのリレーションがどの程度のものかの見当もつく。

4. 四人一組（他者紹介）
   　二人同士のリレーションがついたら、これを四人一組にする。
   　「では自分のパートナーを他の二人のニューフェイスに紹介して下さい」と指示。
   　えっー！というざわめきが起きたがこれは「しまった」という後悔のざわめきである。
   　つまり、つい今しがた聞いていたことを全部忘れてしまい、伝えるべき情報がないからである。
   　ここで義理やおざなりの問いをただす。
   　「社交会話的に聞いていたのは、相手を理解しようという誠意が足りない。今からでも聞き直して、紹介してほしい」と助言。
   　幾分、教室に熱気が出てきた。
   

5. 八人一組
   　さらに今度は八人一組になり、円陣をつくって座る。
   　四人一組同士が対面する座り方でなく、交互にミックスするように指示したのは、集団性が育ちやすいから。
   

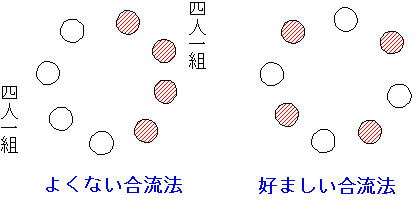
   　隣の人の肩をたたくリレーを右回り、左回りの１回ずつ行ったのは、グループ内のリレーションをつけるため。二つの方法でなければならないという訳ではない。
   　スキンシップという言葉があるように、人は他者に触れたり触れられたりすることで「受け入れられている」という安心感を持つので、このようなエクササイズにした。

6. ブレイン・ストーミング
   　八人一組から代表者一名が出てくるよう指示。
   　すぐには出て来ないのが普通。
   　なぜか。「何をさせられるのだろう」という不安が起きるからである。
   　実際はブレーン・ストーミング用の紙とマジックを渡すために呼んだにすぎないのだが、そのことを云ってないので、尻込みする者が多い。
   　したがって、各グループのリーダーが揃ったところで、「何を命じられるか判らない不安があったと思うが、未知の不安に進んで足を運んだ気概はなかなか大したもの」と賞讃する。
   　このことによって生徒は自分の言動に意識性を持つようになる。
   　またリーダーを通して指示を伝達することで、タテの人間関係が導入される。

7. 共同討議
   　リーダーを通じて渡した紙とマジックを使い、「椅子の座ること以外の利用法を思いつく限り書き出してください」と指示。
   　ここでのねらいは八人の人間による共同討議であって、椅子の利用法以外、古新聞の活用法、校章を思い出して描くなど、なんでもよかった。
   　結果的には傍観者が出てしまい八人の共同討議となったグループは一つだけであった。
   　また、書き出した項目を発表させてみると、思いの外「凶器」だとか「殴る」、「武器」といったバイオレンスなものが目立ち、このクラスに内在する粗野なものを知ることが出来た。

４　対話のある授業

　授業の中にエンカウンターを用いることで何が変わるのか。一言でいうと「対話のある授業」が促進されるということである。対話といっても生徒と教師ばかりではなく、生徒と生徒の対話の方がむしろウエイト的には重くなる。
　再び、５月３０日の指導案に戻りたい。
　前述した導入のエクササイズを経て、いよいよ本時の目標である三角関数のグラフについて学習した。
　最初に指示したことは、発泡スチロールの模型をバラバラにしたピースを手渡し、各グループ毎に「これで何かオブジェをつくってみろ」ということ。

• 条件は、全てのピースを使用すること
• メンバー全員がピースを手に取りオブジェ制作に参加すること

５　実施上の留意点と諸問題

　エンカウンターを授業に利用するときの留意点や諸問題は何かを、実際に授業をしてみた結果から考えてみたい。
　まず、良い点としては授業が談話的雰囲気ですすめられたことをあげたい。測定する尺度があるわけではないので、印象的なことでしか言えないが、知識を教授するといった講義的なムードではなく、ほのぼのとした談話的なムードであった。
　これは生徒同士が教え合っていたことと無関係ではなかろうと思っている。エンカウンターの良さはグループが教育機能を発揮する点にあるからである。
　逆に課題として残ったこともいくつかある。
　ひとつは時間配分。
　通常の50分授業では余程手際よくやるか、導入のエクササイズを厳選しなければタイム・オーバーになってしまうと感じた。実際、指導案にしばられすぎ、もう少し「ゆとり」を持った思考時間を確保してやりたかったという反省がある。
　今回の指導案をこなすには、90〜100分くらいの時間が適当だったかもしれない。
　二点目は、フロアの広さ。
　普通教室で、机・椅子を脇へ寄せて行ったのだが、スペースの狭さはいかんともしがたいものがあった。１クラス40名のエンカウンターといっても、格技室程度のスペースは確保したい。
　狭い教室で、自由に動くこともできず、うずくまるように足を組んでその場から動けない生徒がいたことは最大の反省点である。
　三つ目は、グループ討議の時に傍観者が出てしまったこと。これは一，二点目の反省点に起因するものであるが、エンカウンターのねらいからいって、メンバーの孤立化は絶対に避けなければならない。
　この点については、言葉による交流を制限し、どこかで非言語的コミュニケーションを用いざるを得ないエクササイズをひとつ入れておけば良かったかなと思っている。（「嬉しいときには嬉しい顔をする」、「Ａ君が好きならＡ君のそばに座るようにする」等感情を態度で表出する）
　さらに反省点の四つ目として、学習の転移をあげたい。どういうことかというと、この時間では確かに「ああ」といって知的感動を味わい理解したのだが、それをそのままにとどめてしまった生徒がいたという事実である。
　つまり学習の転移が行われなかったということであり、エンカウンターの時には理解できたものが、持続して定着したものにならなかったということである。
　理解した内容をキチンと再構築しておかないと持続はしない。ただ単にその時間を「あー面白かった」で終えてしまうことになる。
　この点は授業でエンカウンターを利用する上で、今後の実証的研究課題だと思う。
　ただし、そうとは云っても通常の単位円を用いて点をプロットしていく指導法と比較し、明らかに定着率が高まったことは付言しておきたい。

６　教育活動への応用・発展

　エンカウンターはエクササイズが中心となるので、教育活動の様々な場面において機能として発揮できる。
　なにも数学の三角関数のグラフという一分野、一領域に限ったものではない。
　他の分野はもちろん、他教科、ホームルーム活動、生徒会活動、保護者会、職員研修会あるいは生徒指導、進路指導といった具合にあらゆる教育活動とリンクすることができる。
　目的に応じてエクササイズを入れ替えればよいからである。
　エクササイズの配列順序は、抵抗を起こさせないように徐々に深層に迫っていくようにすればよいだけなので、リーダー役の教師の個性によって、様々にバリエーションを変化させられることもまたエンカウンターの魅力となる。
　今回は実施できなかったが、気に入っているエクササイズをいくつか紹介したい。

1. あなたが「魅力的だな」と思うのはどんな人ですか？
   魅力ある人物とは、その人の欲求を満たしている人である。つまり、本人が持ちたいと思いつつ持っていないものを、魅力的な人物は持っているということになる。
   このことによって「自己理解」や「自己受容」が促される。

2. 隣の人の「素敵だな」と思うところを一点あげなさい
   他者の良さが判るとは、自己嫌悪がないということである。自分にコンプレックスのある人は、他者の良い点を認めたがらない。そのことで自分の劣等性が増すからである。逆に自分の性格、容姿、学歴に不満を持っていない人は、他人の性格、容姿、学歴にもあまりクレームを付けない。
   また、他人によい点を指摘してもらうことで自分で気づかなかった、自分の良さを発見することもできる。

3. 高校入学前の出来事で一番悲しかったり、辛かったことはなんですか？
   自分にとって辛かった出来事を人前で喋ることが出来るのは、その出来事を本人が受容しているからである。そういった事実を認めたくない、忘れたいと思っている場合、人前で云うことはない。従って人前で云えるということは、その出来事をもう本人は乗り越えているということになる。
   また「高校入学前」と限定したのは、直近の出来事では生々しすぎることがあるためである。
   さらにこのエクササイズは、他人の人生に対し畏敬の念が湧いてくる。
   苦労したのは自分だけではないことが判り、自分はなんと小さなことでくよくよしていたか、教えられることが少なくない。

　他にもエクササイズは星の数ほど研究実践されているが、それらはエンカウンターの実践紹介とも併せ『エンカウンターで学級が変わる 中学校編 』（図書文化）に詳しいので、そちらに譲ることにしたい。

７　まとめ

　エンカウンターはオールマイティーではない。
　気をつけないと、全体主義化して煽動的になる可能性もある。
　それでも有効な技法であるのは、エンカウンターが「育てるカウンセリング」の一形態だからである。つまり「治すカウンセリング」とは違い、現在時に問題があるわけではないが、今よりももっと、心豊かになることを求めている人を対象に、開発されたものだからである。
　今よりももっと数学に取り組む行動を変容させる。
　今よりももっと数学の魅力に気づく。
　そして、自分でも気づかなかった、自分自身に内在する数学的な能力や素養に気づく。
　そういったことをサイコエジュケーションの立場からアプローチしてみたものである。
　最近は小・中学校における実践報告も多数散見されるが、寡聞にして不勉強のため、道内における高等学校での実践報告をあまり聞かない。
　どうか本レポートを叩き台にして、様々な実証的研究が提示され、よりプラティカルな指導技法が構成されることを願っている。