 2_1 a0を求める
2_1 a0を求める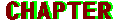 2 波の分解
2 波の分解
 2_1 a0を求める
2_1 a0を求める
先ほどのフーリエ級数式をもう一度確認してみましょう。

この式に出てくるa0の値を、まず求めてみましょう。次の図のように定数波【A】とcos波【B】【C】、sin波【D】が合成された波【E】を考えます。このうち、a0は定数波【A】の値になります。
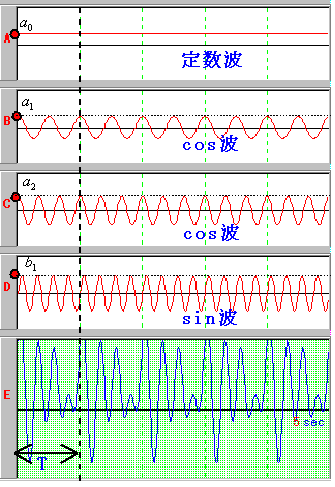
ここで、以前みたように、「合成する波の角速度は合成された波の角速度の整数倍」となりますから、合成された波の1周期分をまず調べればよいことになります。そして、a0の値を求めるために”面積”に着目します。
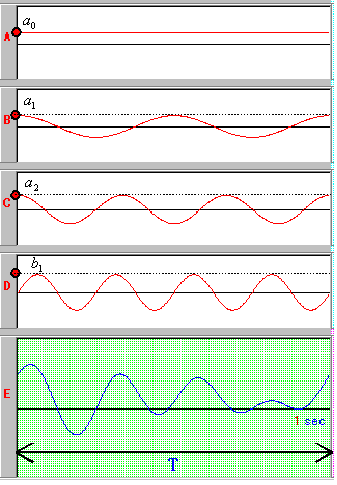
ここで【B】の波をみてください。プラスの部分とマイナスの部分が相殺されて、面積が0になっています。同様のことが【C】と【D】の波についてもいえます。
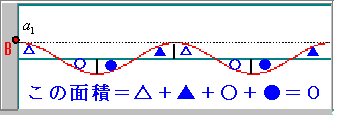
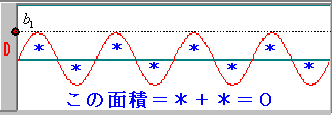
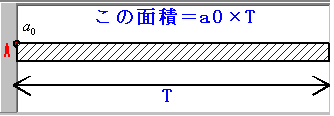
残るのは波【A】のグラフだけとなります。【A】のグラフの面積は、次の図のようにすると、簡単にa0Tと求まります。
これらをまとめると次のようになります。
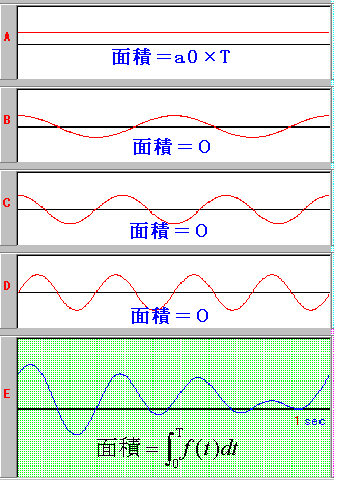
【B】〜【D】の波を合成したものが【E】の波ですから、【E】の面積は【A】の面積、すなわち a0T と同じにならなくてはなりません。これを面積を表す積分記号を用いると、次のようになります。
