丂學悢倎0傪媮傔傞嵺偵丄倎0偵娭偡傞1偮偩偗偺攇傪巆偡偨傔偵乭柺愊乭偵拝栚偟傑偟偨偹丅1廃婜偺娫偵偁傞掕悢攇埲奜偺攇丄偮傑傝倱倝値攇傕們倧倱攇傕柺愊偼慡偰0偵側傝傑偟偨丅
丂偦傟偱偼倎n偵娭偡傞攇丄偡側傢偪們倧倱攇偺柺愊偩偗傪巆偟偰丄偦偺懠偺攇偺柺愊傪0偵偡傞傛偆側曽朄偑偁傞偺偱偟傚偆偐丅
丂偦偙偵搊応偡傞偺偑乭攇偺偐偗嶼乭偲偄偆曽朄偱偡丅師偺僔儈儏儗乕僔儑儞僾儘僌儔儉傪傒偰偔偩偝偄丅嵍懁偼亂A亃乣亂D亃偺4偮偺攇偲偦傟傪崌惉偟偨攇亂E亃偑偁傝傑偡丅塃懁偵偼嵍懁偺亂A亃乣亂E亃偺攇偵1斣忋偵偁傞攇亂W亃傪偐偗崌傢偣偨攇亂A'亃乣亂E'亃偑昞帵偝傟傞傛偆側偭偰偄傑偡丅
丂偙傟傪梡偄偰丄攇偲攇偺偐偗崌傢偣偺婯懃惈傪扵偭偰傒傑偟傚偆丅
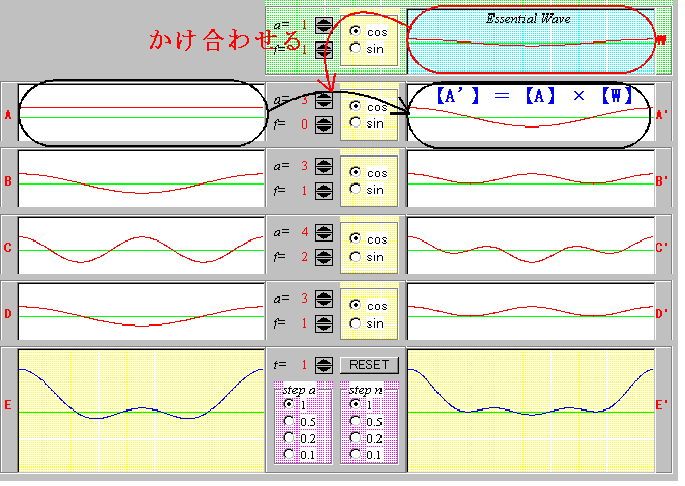
(1)丂們倧倱攇亊們倧倱攇丄倱倝値攇亊們倧倱攇
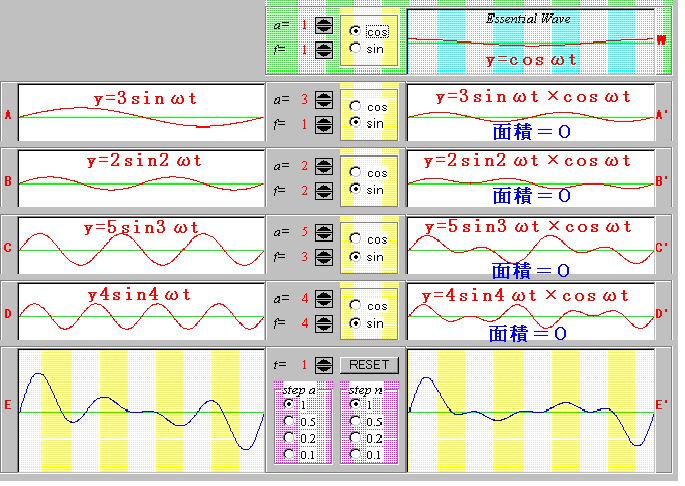
丂傑偢丄婎杮偺攇亂W亃傪們倧倱攇偵偟偰丄們倧倱攇亊們倧倱攇偺條巕傪扵偭偰尒傑偡丅亂A亃乣亂D亃偺攇偺廃攇悢傪偄傠偄傠曄偊偰僔儈儏儗乕僩偟偰傒傑偟傚偆丅
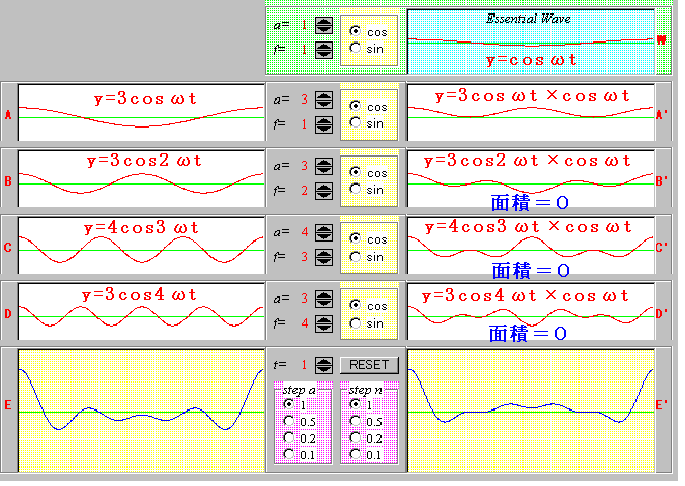
丂偙偺僔儈儏儗乕僩偵傛傝婎杮偺攇亂W亃偺廃攇悢偲摨偠廃攇悢傪帩偮們倧倱攇偺柺愊偩偗偑巆傝丄偦傟埲奜偺攇偺柺愊偼0偵側傞偺偑暘偐傝傑偡丅
丂們倧倱攇偲摨條偺偙偲偑倱倝値攇偵偮偄偰傕偄偊傑偡丅
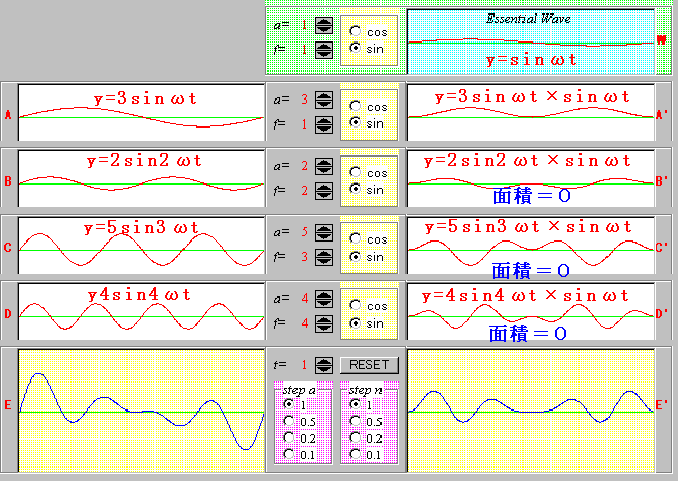
丂埲忋偺偙偲傪傑偲傔傞偲師偺傛偆偵側傝傑偡丅
|
們倧倱攇亊們倧倱攇乮倱倝値攇亊倱倝値攇乯偺柺愊 丂丂嘆廃攇悢偑摨偠偲偒丂丂亄 丂丂嘇廃攇悢偑堘偆偲偒丂丂侽 |
(2)丂倱倝値攇亊們倧倱攇
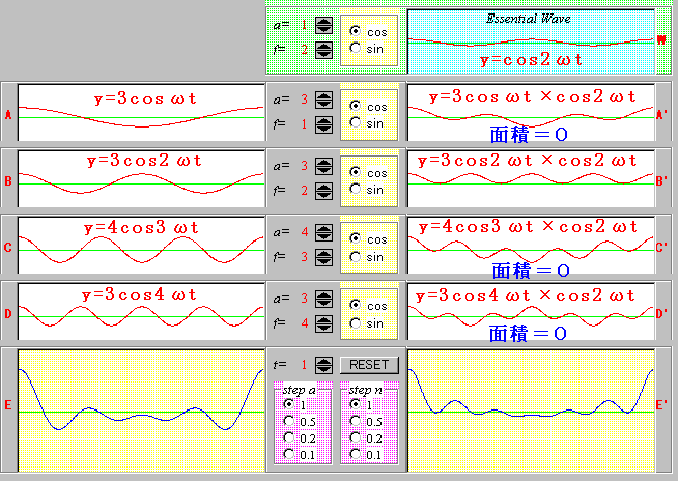
丂偦傟偱偼倱倝値攇偲們倧倱攇偺偐偗嶼偼偳偆偱偟傚偆偐丅婎杮偺攇亂W亃傪傑偢們倧倱攇偵偟偰丄亂A亃乣亂D亃偺攇傪廃攇悢偺堘偆倱倝値攇偵偟偰傒傑偟傚偆丅偙傟傪傒傞偲丄偐偗崌傢偝傟偨攇偼偳傟傕柺愊偑侽偵側偭偰偄傑偡丅
丂摨條偺偙偲偑婎杮攇傪倱倝値攇偵偟偰丄偐偗崌傢偣傞攇傪們倧倱攇偵偟偨応崌偵傕惉傝棫偪傑偡丅
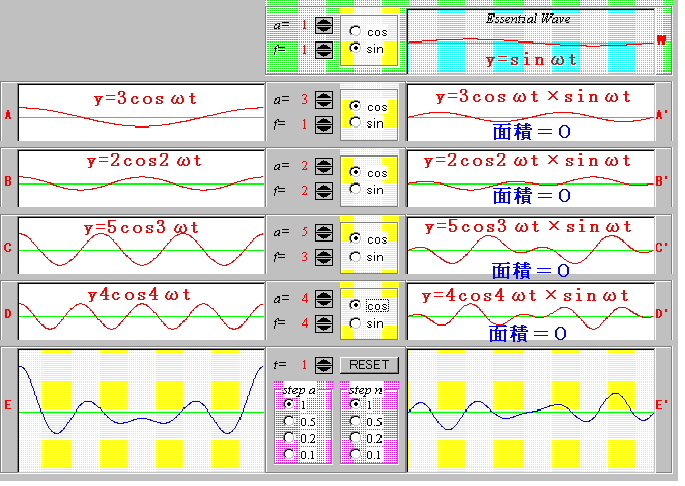
| 們倧倱攇亊倱倝値攇偺柺愊亖侽 |
丂(1)偲(2)傪傑偲傔傞偲丄柺愊傪巆偡偵偼
| 摨偠廃攇悢偺們倧倱攇乮傑偨偼倱倝値攇乯傪偐偗崌傢偣傞 |
偲傛偄偙偲偑暘偐傝傑偟偨丅
|
僔儈儏儗乕僔儑儞僾儘僌儔儉偺僟僂儞儘乕僪 仢幚峴僾儘僌儔儉乽add_wave.exe乿乮栺63KB乯 仢僇僗僞儉僐儞僩儘乕儖乽Spin32.ocx乿乮栺52KB乯 佀乽Spin32.ocx乿偼Windows\System僼僅儖僟偵抲偄偰偔偩偝偄 |
 2_2丂攇偺偐偗嶼
2_2丂攇偺偐偗嶼