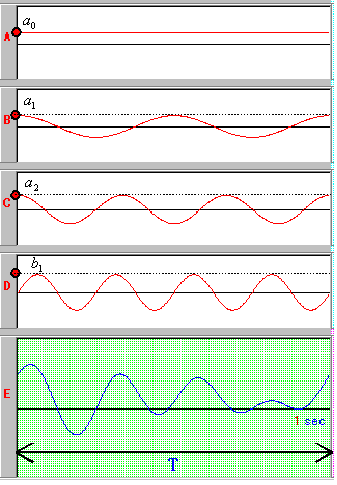
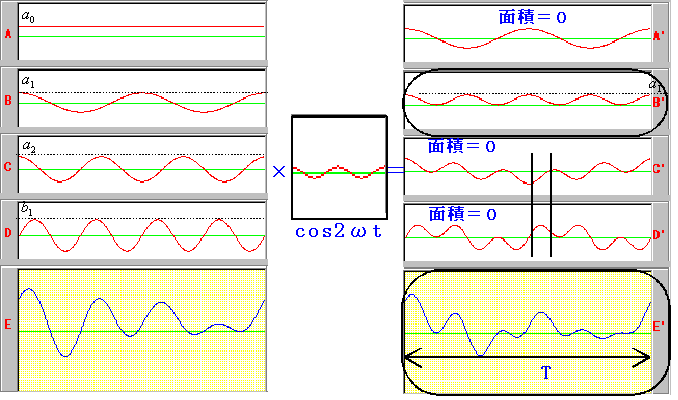
先ほどみたように、波の面積を残すには「同じ周波数のｃｏｓ波（またはｓｉｎ波）をかけ合わせる」とよいことがわかりましたね。ですから【B】の波の面積を残すために、1周期の波の数が2のｃｏｓ波　ｃｏｓ2ωt　の波をかけ合わせてみましょう。かけ合わされた波【B'】の面積＝【E'】の面積となります。

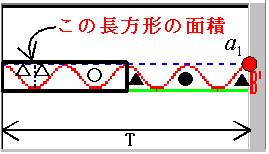
　さて、では【B'】の波の面積はどうやって出せばよいのでしょうか。この部分の面積を出すのは、▲→△、●→○に移動させると、たてａ₁、よこＴ/2の長方形の面積、すなわちａ₁×Ｔ/2と同じになります。

　これを積分記号を用いて表すと、

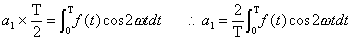
　フーリエ級数の展開式の一部が、遂に姿を現しましたね。同様にすれば、その他の係数も求めることができます。