【TOP】 【BACK】 【NEXT】

４．The secret of the changes

　Next, Consider the secret of the changes. It is possible to make changes a numerical formula.
　For details, look at " The Tail of Mobius " by Mr.Nakamura.
　For example,consider w=z2.
　　　Let z=x+yi.
　Consider how three straight lines, y=0,1,2 have been changed in figure 1.
　Consider how three straight lines, x=−1, 0, 1,have been changed in the same way in figure 2.
　In both next figures, lines are changed into the parabolas which have their focus at the origin. Also there are pseudo-axis in the real plane associated with parabolas.
　Only two curves appear when changing the three lines of x=−1, 0, 1. This is because the lines x=-1 and a=1 were changed in the same way, so these curves over cap.

change of a level straight line change of a perpendicular straight line synthesizes a changed straight line


　How the other changes made? Let's attempt to think of a typical change.

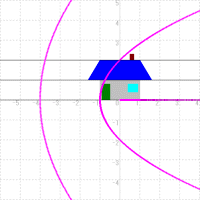
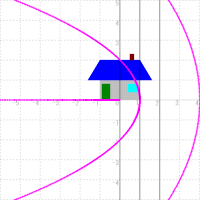
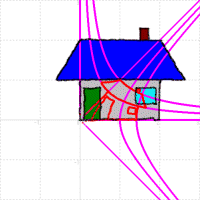
○ In case of w=√z

　Like the following figure, the straight line which is parallel to the real axis is shifted to the rectangular hyperbola, the asymptote of which is x axis and y axis.
　Also, the straight line which is perpendicular to the real axis is shifted to the one in the neighborhood of the origin. In addiotion, it is turned by −45 degrees.

○ In case of w=1/z

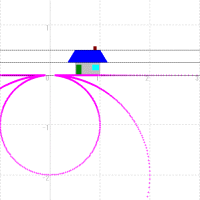
　Like the following figure, the straight line which is parallel to the real axis is shifted to the circle which has a center and a diameter on the y axis.
　Also, the straight line which is perpendicular to the real axis is shifted to the circle which has a center and a diameter on the x axis.

○ In case of w=ez

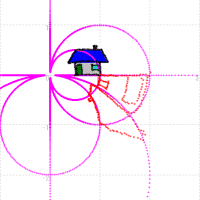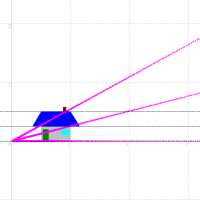
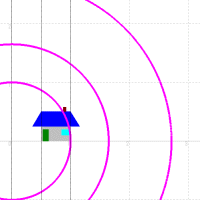
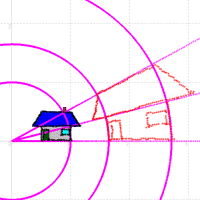
　Like the following figure, the straight line which is parallel to the real axis is shifted to the straight line which passes the origin.
　Also, the straight line which is perpendicular to the real axis is shifted to the circl which has a center to the origin.

【TOP】 【BACK】 【NEXT】