侾丏2師曽掱幃偺嫊悢夝偺僀儊乕僕壔
 丂堦斒偵幚學悢偺俀師曽掱幃 f(x)亖0偺幚悢夝偼丆xy暯柺忋偵偍偗傞y亖f(x) 偺僌儔僼偲x幉偲偺嫟桳揰偺x嵗昗偱偁傞丅偟偐偟丆嫊悢夝偺偲偒偺偦偺幚懺偼傢偐傝偵偔偄丅嫊悢夝傪幚悢夝偺傛偆偵僀儊乕僕壔偡傞曽朄傪峫偊偰傒傛偆丅
丂堦斒偵幚學悢偺俀師曽掱幃 f(x)亖0偺幚悢夝偼丆xy暯柺忋偵偍偗傞y亖f(x) 偺僌儔僼偲x幉偲偺嫟桳揰偺x嵗昗偱偁傞丅偟偐偟丆嫊悢夝偺偲偒偺偦偺幚懺偼傢偐傝偵偔偄丅嫊悢夝傪幚悢夝偺傛偆偵僀儊乕僕壔偡傞曽朄傪峫偊偰傒傛偆丅
丂嬶懱揑偵師偺娭悢傪椺偵偲偭偰峫偊偰傒傞丅
丂丂y=x2亅2x+5ゥ@
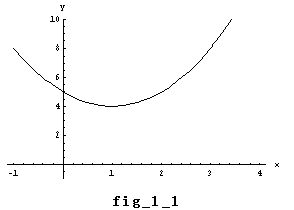
丂y=(x亅1)2+4 傛傝丆x偑幚悢偺偲偒僌儔僼偼fig_1_1偺傛偆偵側傞丅
丂偙偺偲偒丆曽掱幃
丂丂x2亅2x+5亖0ゥA
偼幚悢夝傪帩偨側偄丅夝偼x亖1亇2i 偲偄偆嫊悢夝偵側傞丅
 丂偦傟偱偼x傪嫊悢夝偲峫偊x=u+vi (u丆v 偼幚悢) 偲偟偰傒傞偲丆
丂偦傟偱偼x傪嫊悢夝偲峫偊x=u+vi (u丆v 偼幚悢) 偲偟偰傒傞偲丆
丂丂 y亖(u亄vi)2亅2(u亄vi)亄5
丂丂丂亖u2亄2uvi亅v2亅2u亅2vi+5
丂丂丂亖(u2亅v2亅2u+5)亄2v(u亅1)iゥB
丂y偑幚悢偵側傞応崌傪峫偊傞偲丆
丂丂2v(u亅1)亖0丂丂丂亪 v亖0 傑偨偼 u=1ゥC
丂偙偺偲偒丆y偺幚悢晹暘 Real y 偼丆
丂丂 Real y=u2亅v2亅2u+5ゥD
偲側傞丅
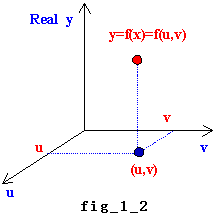
丂偙偙傑偱傪恾帵偟偰傒傞丅x=u+vi 偼 u丆v傪椉嵗昗幉偵偲偭偨暯柺乮暋慺暯柺乯忋偺揰 (u丆v) 偱昞傢偝傟傞丅
 丂偦偟偰丆偦偺尨揰O偱偙偺暯柺偵悅捈偵幚暯柺傪棫偰偨嬻娫傪峫偊丆偦偺3師尦嬻娫偱 y=f(x)=f(u丆v) 偺僌儔僼傪峫偊傟偽椙偄偙偲偵側傞丅 (fig_1_2嶲徠)
丂偦偟偰丆偦偺尨揰O偱偙偺暯柺偵悅捈偵幚暯柺傪棫偰偨嬻娫傪峫偊丆偦偺3師尦嬻娫偱 y=f(x)=f(u丆v) 偺僌儔僼傪峫偊傟偽椙偄偙偲偵側傞丅 (fig_1_2嶲徠)
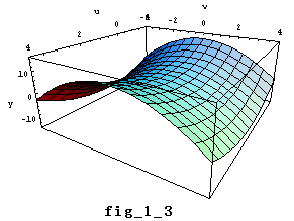
丂嘍偺Real y=u2亅v2亅2u+5 偺僌儔僼偼fig_1_3偺傛偆偵側傞丅
丂偙偙偱丆嘋偺2偮偺応崌傪峫偊偰傒傛偆丅
(1) v=0偺偲偒 (x偑幚悢偺偲偒)
丂丂嘍傛傝丂Real y=u2亅2u+5 偲側傝丆x=u+vi=u 偩偐傜
丂丂Real y=u2亅2u+5= x2亅2x+5
丂偙傟偼fig_1_1偱帵偝傟偰偄傞傕偺偲摨偠幚悢夝傪帩偮応崌偱偁傞丅
丂偙偺偙偲傪暿側妏搙偐傜僀儊乕僕壔偡傞偲師偺傛偆偵側傞丅愭傎偳偺3師尦嬻娫忋偺
丂丂嬋柺 Real y=u2亅v2亅2u+5 偲暯柺v=0
偺岎慄傪峫偊傞丅偙偺岎慄偙偦uy暯柺 (xy暯柺)忋偺曻暔慄偱偁傞丅(fig_1_4嶲徠)
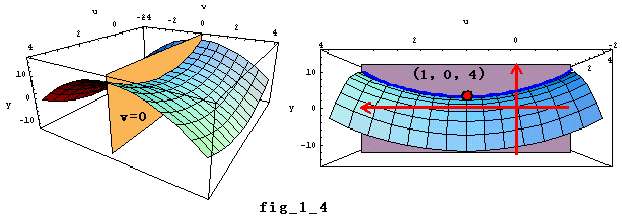
(2) u=1偺偲偒
丂嘍傛傝 Real y=u2亅v2亅2u+5=1亅v2亅2+5亖亅v2亄4
丂偙偙偱y亖0偲側傞偺偼丆亅v2亄4亖0傛傝 v亖亇2
丂偡側傢偪y亖0偲側傞揰偼uv暯柺偲偺岎揰 (1丆亇2) 丆偮傑傝x亖1亇2i 偱丆偙傟偑嘇偺曽掱幃
丂丂x2亅2x+5亖0
偺夝偲側傞丅
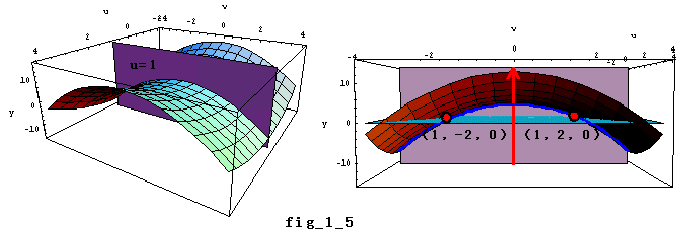
丂偙偺偙偲傪傑偨3師尦嬻娫忋偺僀儊乕僕偲偟偰曔傜偊偰傒傛偆丅崱搙偼師偺2偮偺恾宍偺岎慄偲峫偊傜傟傞丅
丂丂嬋柺 Real y=u2亅v2亅2u+5 偲暯柺 u=1
丂偙偺岎慄乮曻暔慄乯偲暯柺 y亖0偺岎揰偑 (1丆亇2丆0) 偲側傞丅 (fig_1_5嶲徠)