２．3次方程式の虚数解のイメージ化

　3次以上の方程式についても，同様な方法でイメージ化することができる。

　次のような簡単な3次方程式を考える。

　　x³+8=0･･･�@

　この方程式の解は x=-2，1i となり、

　　y=x³+8･･･�A

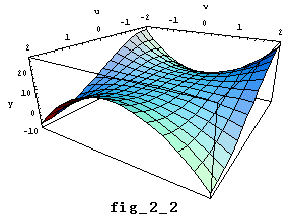
のグラフは fig_2_2 のようになる。この x軸との交点 -2 が実数解である。それでは残りの虚数解のイメージ化を考えよう。

　x=u+vi (u，v は実数) とおくと，

　　 y＝(u＋vi)³+8

　　　＝u³＋3u²vi+3uv²i²+v³i³+8

　　　＝u³＋3u²vi-3uv²-v³i+8

　　　＝(u³−3uv²+8)＋v(3u²−v²)i･･･�B

　yが実数になる場合を考えると，

　　v(3u²−v²)＝0

　　　∴ v＝0 または 3u²−v²=0･･･�C

　このとき，yの実数部分 Real y は，

　　 Real y=u³−3uv²+8･･･�D

となる。この平面はfig_2_2のようになる。

　ここで，�Cの2つの場合を考えてみよう。

(1) v=0のとき (xが実数のとき)

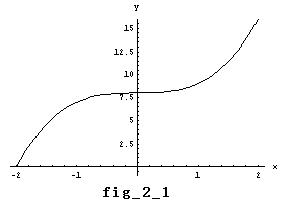
　　�Dより　Real y=u³+8 となり，fig_2_1で示されているものと同じ実数解を持つ場合である。

　このことを別な角度からイメージ化すると次のようになる。先ほどの3次元空間上の

　　曲面 Real y=u³−3uv²+8 と平面 v=0

の交線を考える。この交線こそuy平面 (xy平面)上の曲線となる。今度は平面 y=0 との交点（-2，0，0）が1つ存在することが分かる。これが x³+8=0 の実数解なのである。(fig_2_3参照)

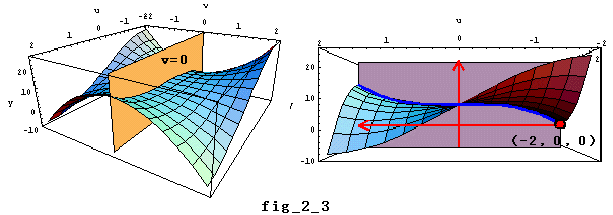
(2) 3u²−v²=0　すなわち v=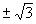u のとき

　�Dより Real y=u³−3uv²+8=u³-9u³+8=-8u³+8

　ここでy＝0となるのは，−8u³＋8＝0より u＝1 (uは実数），v=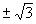

　すなわちy＝0となる点はuv平面との交点 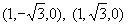，つまりx＝1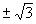i で，これが�Aの方程式　x³+8＝0　の虚数解となる。

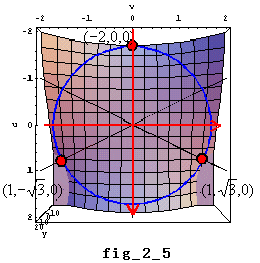
　このことをまた3次元空間上のイメージとしてとらえると、今度は次の3つの図形の交線と考えられる。

　　曲面 Real y=u³−3uv²+8 と平面 v=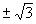u

　この交線（放物線）と平面 y＝0の交点が 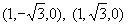となる。 (fig_2_4参照)

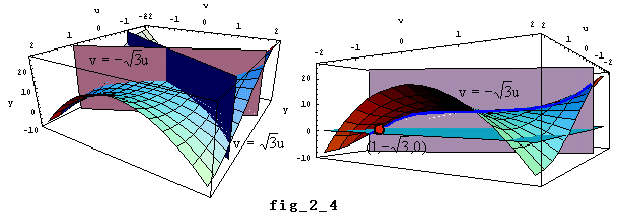
　(1)(2)をまとめてうえから見た図が fig_2_5 である。uv平面上でこれらの3点は、原点を中心として半径2の円周上に、中心角120°の間隔で並んでいる。つまり円周の3等分点になっているのである。