同一直線上にない3点O，A，Bに対して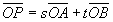， が次の条件を満たすとき，終点Pの存在する範囲を求めよ。 　(1) s+t=1　　　(2) 2s+3t=6　　(3) s+t≦2，s≧0，t≧0　　　(4) −1≦s≦1，−1≦t≦1

　

　終点Ｐの存在範囲を求める問題はなかなか指導が困難な教材の１つです。(2)の解答は

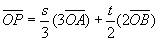　　　より
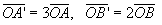　　　とすると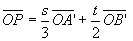　　
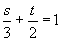　　　　より　直線A'B'

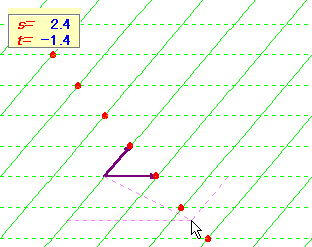
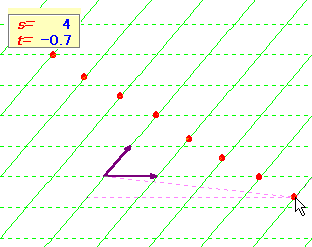
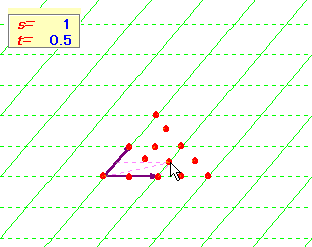
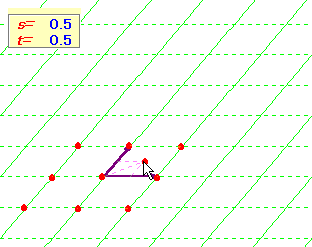
となるでしょうか。しかし，「s+t=1 ならば 点Pは直線AB上」という関係だけが先行するのであれば，あまり意味がない気がします。問題はどの様にイメ−ジとして自分の中で消化できるか，というところだと思います。そのためには具体的に条件を満たすs,tの値を考え，点Pをプロットしてみることが大事です。ここに上げた問題以外にもいろいろなパタ−ンを考えれば，かなりの練習量になります。

　また，具体的に問題をこなしていけば，端点をとれば図形が図示できることが理解でき，さらにベ−スの変換（斜めの座標系）の理解にもつながっていきます。