|
平面上に1直線上にない3点O,A,Bが与えられ,OA=2,OB=3とする。 (1) 実数s,tがs≧0,t≧0,0≦s+t≦1を満たしながら変わるとき,ベクトル 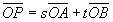 の終点Pが動く領域の面積を求めよ。 の終点Pが動く領域の面積を求めよ。(2) 点Pが(1)の領域を動き,点Qが点Aを中心とする半径1の円の内部を動くとき,ベクトル 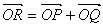 の終点Rが動く領域の面積を求めよ。 の終点Rが動く領域の面積を求めよ。(89年 北見工大,改題)
|
 これは以前入試で出題された問題です。(2)の問題はなかなか生徒には難しい問題といえます。この問題こそ,題意をきちんと理解できるか,イメ−ジとして具体化できるか,が問われる問題といえるでしょう。
これは以前入試で出題された問題です。(2)の問題はなかなか生徒には難しい問題といえます。この問題こそ,題意をきちんと理解できるか,イメ−ジとして具体化できるか,が問われる問題といえるでしょう。![]() のようにきちんとイメージ化できていなくては,なかなか難しいでしょう。
のようにきちんとイメージ化できていなくては,なかなか難しいでしょう。
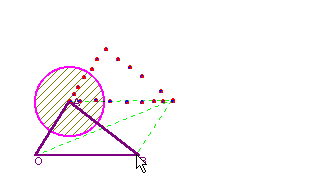
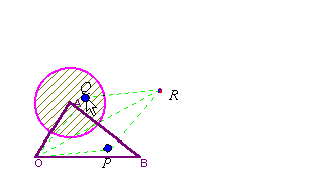
先ほどと同様にどちらか1点を固定させて考えてみましょう。下の図は,まず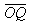 を固定して
を固定して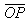 を変化させているものです。点Pが△OAB内を動くとき,終点Rは△OABを平行移動させた図形内を動くのがよくわかります。同様にして
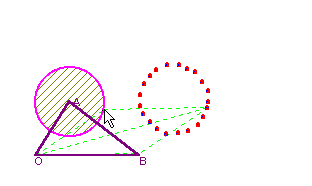
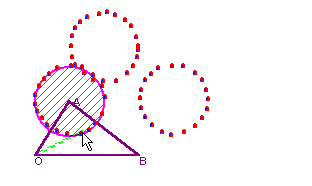
を変化させているものです。点Pが△OAB内を動くとき,終点Rは△OABを平行移動させた図形内を動くのがよくわかります。同様にして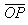 を固定して
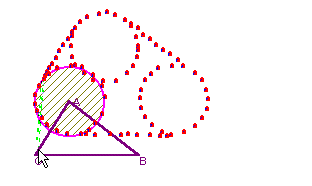
を固定して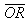 を動かすと平行移動した先に円を描くのがわかります。やはり,イメ−ジとしてどれだけすぐにとらえられるか,が問題となります。
を動かすと平行移動した先に円を描くのがわかります。やはり,イメ−ジとしてどれだけすぐにとらえられるか,が問題となります。