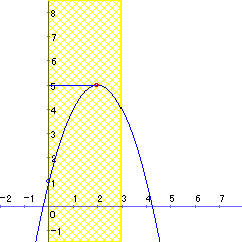
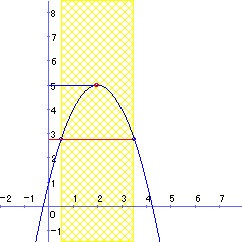
次の問いに答えよ。 (1) 2次関数 f(x)＝−x2＋4x＋1の0≦x≦aにおける最大値と最小値を場合分けして求めよ。 (2) 2次関数 y＝x2−4x＋1のt≦x≦t＋1 における最小値を m とするとき，関数 y=m(t)のグラフを描け。

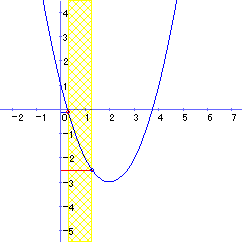
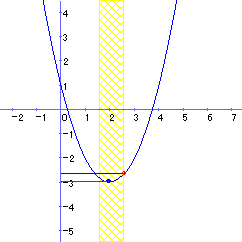
　(2)は定義域がtの値と共に変化する場合の最小値を求める問題です。生徒にとっては区間が変化するために，場合分けを余儀なくされます。最も思考力を発揮せねばならない問題です。授業の中で教える場合，どういった場合があるのかを板書するのはなかなか大変です。1つのグラフに描けば見ずらくなり，場合に分けていくつも図示すると手間がかかる。最もコンピューターが得意とする分野だといえます。

　また，y=m(t) のグラフを描く場合，生徒にとっては完全に y=f(t) のグラフとかけ離れた存在となりがちですが，y=f(t) のグラフと，y=m(t)のグラフを同時に見せることにより，tが時間の変数として，同時に変化する様子も良くわかります。