1. 陽関数のグラフ
   

   次の関数のグラフを描け。 (1) y=ax2+bx＋c　　　 (2) y=｜x2-2x｜+x-2

   
   (Calculator)
   (1) y1=ax^2+bx+c　　　　　(2) y1=Abs(x^2-2x)+x-2

   　
   

2. 陰関数のグラフ
   

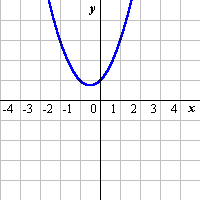
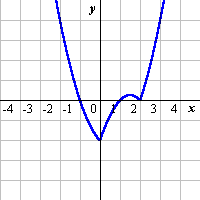
   次の関数のグラフを描け。 (1) x2+y2=16　　　　 (2) y2=4sx

   
   (Calculator)
   (1) 0=x^2+y^2-16　　　　　(2) 0=y^2-4sx

   　
   

3. 極値の描くグラフ
   

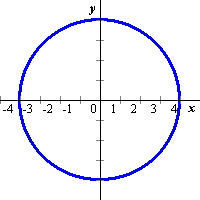
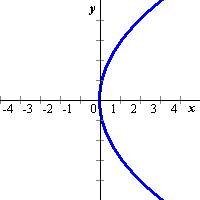
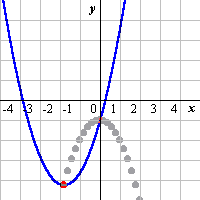
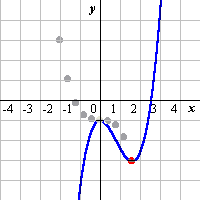
   次の関数の極値の描く関数を求めよ。 (1) y=x2+2ax＋b　　　　 (2) y=x3+3ax2＋b

   
   (Calculator)
   (1) y1=x^2+2ax+b　点Ｐ　x=-a　y=-a^2+b　または　f(x)=x^2+2ax+b　y1=f(x)　y2=(f'(x)=0)f(x)
   (2) f(x)=x^3+3ax^2+b　y1=f(x)　y2=(f'(x)=0)f(x)

   　
   

4. 軌跡の方程式
   

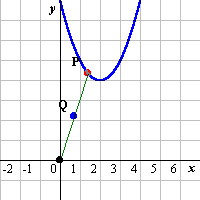
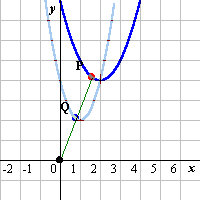
   原点Ｏと放物線 y=(x-2)2+4 上の点Ｑとを結ぶ線分ＯＱの中点をＰとする。この点Ｑが放物線上を動くとき，点Ｐの描く図形の方程式を求めよ。

   
   (Calculator)
   f(x)=(x-2)^2+4　　y1=f(x)
   点Ａ　x=0　y=0　　点Ｐ　x=a　y=f(a)　　点Ｑ　x=Px/2　y=Py/2
   点Ａと点Ｐを線で結ぶ

   　
   

類　題

1. 次の関数のグラフを描け。
   (1) y=a sin(bx+c)　　　 (2) y=log_ax

2. 次の関数のグラフを描け。
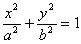   (1) 　　　　　 (2) x³+y³=3axy

3. 関数 y=x⁴+ax³＋2 の極値の描く関数を求めよ。

4. 点Ａ(-4，0)と点(2，0)を中心とする円上の点Ｑとを結ぶ線分ＡＱを2：1に内分する点をＰとする。この点Ｑが円上を動くとき，点Ｐの描く図形の方程式を求めよ。