マスオ博士，今学校で因数分解を習っているんだけど，分からないところがあるんです。最後に文字のいっぱい入った式の因数分解が出てくるんですけど，全然わからないんです。

　


おやおや，初めから泣き顔かい。文字のいっぱい入った式，というと例えば
　　　ｘ2＋３ｘｙ＋２ｙ2−ｘ−３ｙ−２
こんな式のことかい？



そうです，博士！
学校の先生は最低次の文字で整理して・・・
そして・・・
たしか，たすきがけを連発していたような・・・


なるほど。確かに面倒なやり方だね。それでは，もう少し簡単な方法を考えてみようかな。
その前にもう一度たすきがけをおさらいしておこう。
マティカ君，次の式は因数分解できるかな？
　　　２Ｘ2＋７Ｘ＋３
博士，それならできます。

　　　

こんな風に，たすきがけして，答えは
　　　(ｘ＋３)(２ｘ＋１)
です。


ちゃんと，たすきがけは理解しているようだね。このたすきがけを次のような表で表わしてみよう。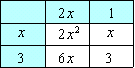

この表の作り方を説明しよう。まず ２ｘ2＋７ｘ＋３ の ２ｘ2 に目を付けて ｘ と ２ｘ に分解する。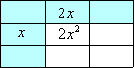

　⇒　

次に最初の ３ の数字を １ と ３ に分解する。これを表にすると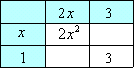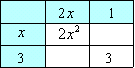

　　　

この様に２通り考えられるね。それぞれ行と列を掛け合わせて空欄を埋めると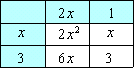

　⇒　

それぞれの表で ｘ の項を計算すると
　　左の表では　２ｘ＋３ｘ＝５ｘ，　右の表では　６ｘ＋ｘ＝７ｘ
問題の式は ２ｘ2＋７ｘ＋３ だったから，右側の表が正解になるわけだよ。
つまり答は１列目と１行目から
　　　(ｘ＋３)(２ｘ＋１)











なるほど，博士！　分かったけど，これならたすきがけとほとんど同じだと思うんだけど・・・。

これだけだと，わざわざ表にかく必要もないね。そこで本題に入ろう。
　　　ｘ2＋３ｘｙ＋２ｙ2−ｘ−３ｙ−２
この式の因数分解を考えてみよう。
次のような表を作るんだ。簡単のために３箇所を埋めておいたよ。

　　　　　

先ほどの要領で表を埋めてご覧，マティカ君。