この表を埋めればいいのね。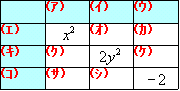

まるでパズルみたいね。まず(ｱ)と(ｴ)が埋まるわ。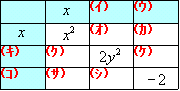

まだいっぱいあって，どこから手をつけていいのかしら。




それではヒントを出そう。２ｙ2を分解することを考えてご覧。
　　　ｘ2＋３ｘｙ＋２ｙ2＋・・・
の＋３ｘｙ に目を付けて(ｲ)と(ｷ)を埋めることができないかな？

本当だ！　２ｙ2 は ２ｙ×ｙ しかないから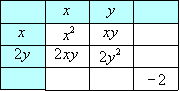

これだとｘｙの項が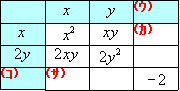
　　　２ｘｙ＋ｘｙ＝３ｘｙ
でピッタリ！！！
あともう少しね。次は−２の番だわ。−２は
　　　２×(−１)，−２×１，１×(−２)，−１×２
の４通りあるけど・・・


　　　ｘ2＋３ｘｙ＋２ｙ2−ｘ−３ｙ・・・
この式の −ｘ に目を付けると(ｶ)と(ｻ)で−１になればいいわけね。つまり(ｳ)に−２，(ｺ)に１をいれればＯＫ！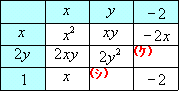

最後に２つ空いているけど(ｼ)がｙで(ｹ)が−４ｙだから
　　　ｙ−４ｙ＝−３ｙ
やったあ！　ピッタシ！！　つまり答えは
　　　(ｘ＋２ｙ＋１)(ｘ＋ｙ−２)



いつのまにか１人でやっていたようだね。どうだいマティカ君。やり方を変えれば少しは理解の手助けになったかな。