さて問題は，ディスク１０枚を動かすときに何回でできるか，ということだったね。
さすがに１０枚を動かしてみるのは大変だね。さっきは３枚までやったから，とりあえず次の４枚でやってみよう。
人生一歩いっぽあせらず進んでいくことが大切なんだよ。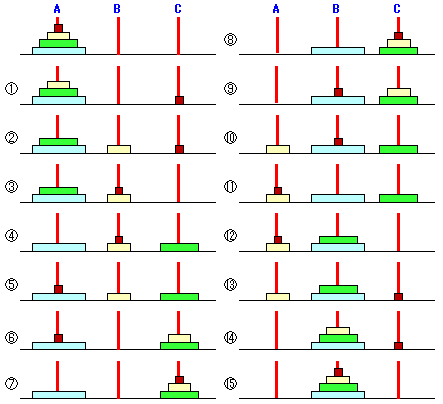




博士すごーい!!　４枚だと１５回も動かさなきゃいけないのね。
４枚でさえ大変なのに，１０枚なんてとても無理です，博士。
そうだね。とても気の遠くなる話しだね。
そこで今までのことから何か推測できないか考えてみよう。さっきは１枚の場合はやってなかったけど，１枚を動かすのは当然１回だね。１枚から４枚までのディスクを動かすのに必要な回数をまとめると，次のようになるよ。

枚数１２３４５
回数１３７１５？

ここから５枚のディスクだと何枚になるか推測できないかな？



数字の間の関係を考えるのね。
うーん。難しいわ。
博士，私が数学苦手なのよく知ってるでしょ！

よーし。それでは少しヒントを出そう。下の数字に１を足してみよう。
どうだい，何か気づかないかい。

回数＋１２４８１６？



博士，それならわかるわ。
２倍していけばいいわけだから，次は３２になるのね。
その通り。このように規則正しく並んだものを数列というんだよ。
さて１０枚のときの回数を求めるために，少し難しいけど今の数字を別な書き方をしてみよう。

２４８１６３２・・・
↓↓↓↓↓　
２1２2２3２4２5・・・


博士，わかったわ！　１０枚だと２10になるのね。
２10は２を１０回かければいいわけだから，２×２×・・・
えーと，面倒だから電卓を使っちゃえ。
　　　・・・・・・
博士出ました。１０２４です。つまり１０２４回でできるんですね。

マティカ君，何か大事なことを忘れていないかい。
さっき回数に１を足したよね。
借りたものは返さないといけない。これを世の中では「貸し借りの法則」というんだ。

博士，わかりましたよ。返しますよ，ちゃんと。これでもそういうところはしっかりしているんですからね。
つまり１０枚のディスクを動かすには
　　　２10−１＝１０２３　回
必要なんでしょ。
でもやっぱり，丸ごと１回で動かす方が私にはあってるわ。

まあ，そういわずに。目標の１０枚のときの回数が出たわけだから…。
ところでさっき何気なく“１”を足したね。
その“１”という数字はどこから出てきたんだろうね。
それは学校の授業でしっかりと勉強してくださいね。