 |  |
嘆昁梫惈偲庤寉偝
嘆僷儔儊乕僞傪曄壔偝偣傞
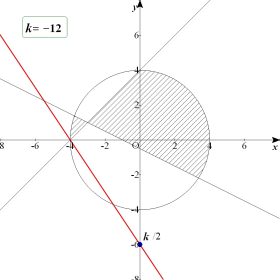
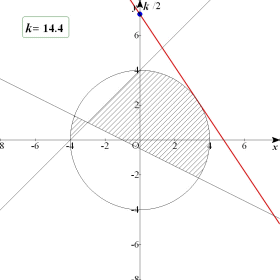
| 楢棫曽掱幃 (x亅y亅4)(x亄2y亄1)亞0丆x2亄y2亝16 偺昞偡椞堟傪峫偊傞丅揰 (x,y) 偑偙偺椞堟傪摦偔偲偒丆3x亄2y 偺嵟戝抣偲嵟彫抣傪媮傔傛丅 |
 |  |
嘇婳愓傪梡偄傞
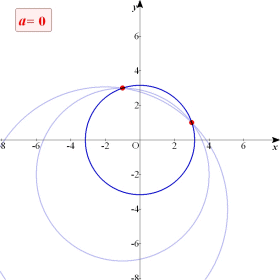
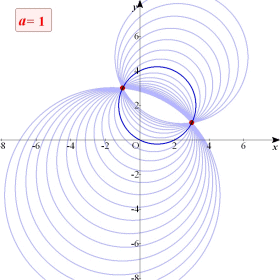
| 墌 x2亄y2亅2ax亅4ay亄10a亅10亖0偑丆掕悢a偺抣偵娭傢傜偢捠傞2掕揰傪媮傔傛丅傑偨偙傟傜偺墌偺偆偪丆敿宎偑嵟彫偲側傞帪偺a偺抣傪媮傔傛丅 |
 |  |
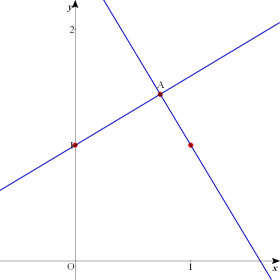
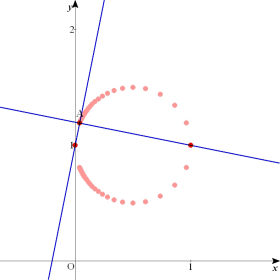
| 揰 (1丆1) 傪捠傞捈慄h偲捈慄 g丗y亖ax亄1 偲偑岎揰A偱悅捈偵岎傢傞偲偡傞丅a偑幚悢慡懱傪摦偔偲偒丆岎揰A偺嵗昗偍傛傃婳愓傪媮傔傛丅 |
 |  |
嘊嵶偐側晹暘傪夝愅
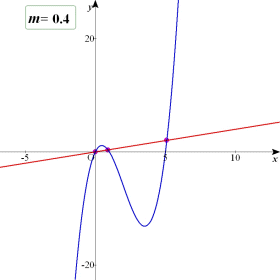
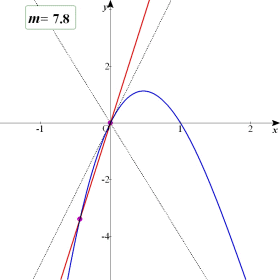
| 嬋慄y亖x3亅6x2亄5x 偲捈慄 y亖mx 偲偑憡堎側傞3揰偱岎傢傞偨傔偺m偺忦審傪媮傔傛丅 |
 |  |
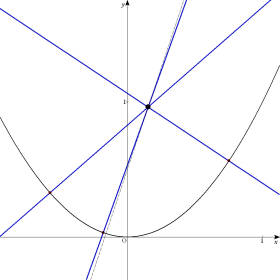
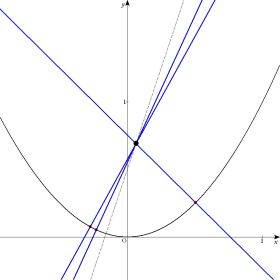
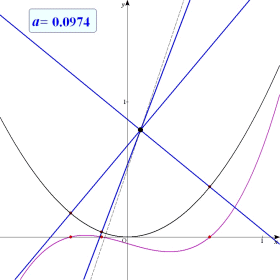
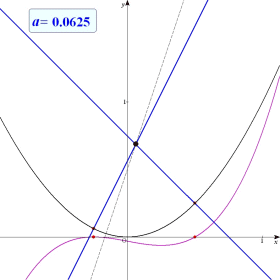
| 捈慄 y=3x+1/2 忋偺揰 (p丆q) 偐傜曻暔慄 y亖x2 偺朄慄偼壗杮堷偗傞偐挷傋傛丅 |
 |  |
 |  |
嘋僀儊乕僕偟偯傜偄晹暘傪夝愅
| xy暯柺忋偺揰 P(x丆y) 偺嵗昗偑丆x亖u亄v丆y亖uv 偺宍偱梌偊傜傟偰偄傞偲偡傞丅u丆v 偑 0亝u亝1丆0亝v亝1 偺斖埻傪摦偔偲偒丆揰P偺捠夁偡傞斖埻傪恾帵偣傛丅 |
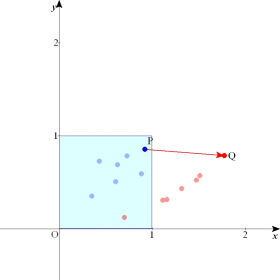 | 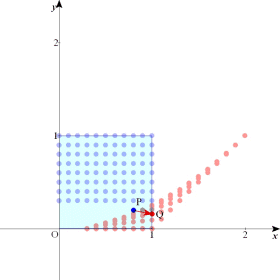 |
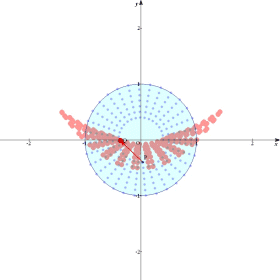 |  |
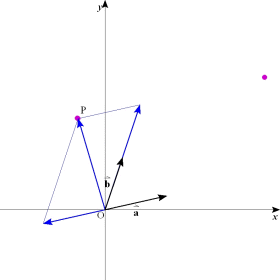
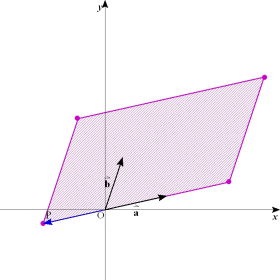
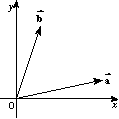 塃偺恾偺傛偆側儀僋僩儖
塃偺恾偺傛偆側儀僋僩儖 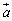 丆 丆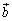 偑偁傞丅幚悢s丆t傪偲傝丆儀僋僩儖 偑偁傞丅幚悢s丆t傪偲傝丆儀僋僩儖 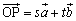 偲偡傞丅幚悢s丆t偑丆亅1亝s亝2丆0亝t亝2 偺斖埻傪摦偒偲偒丆揰P偺懚嵼斖埻傪恾帵偣傛丅 偲偡傞丅幚悢s丆t偑丆亅1亝s亝2丆0亝t亝2 偺斖埻傪摦偒偲偒丆揰P偺懚嵼斖埻傪恾帵偣傛丅
|
 |  |
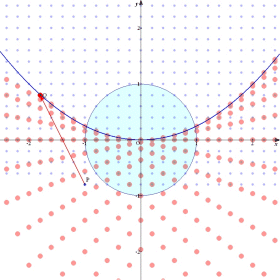
嘍戣堄傪偮偐傑偣傞
暯柺忋偵1曈偺挿偝偑1偺惓嶰妏宍偑偁傞丅t傪幚悢偲偡傞偲偒丆暯柺忋偺揰P偱丆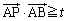 偐偮 偐偮 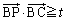 偐偮 偐偮 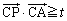 傪枮偨偡傕偺慡懱偐傜側傞椞堟傪 D(t) 偲偍偔丅 傪枮偨偡傕偺慡懱偐傜側傞椞堟傪 D(t) 偲偍偔丅(1) 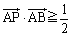 傪枮偨偡揰P偐傜側傞椞堟傪恾帵偣傛丅 傪枮偨偡揰P偐傜側傞椞堟傪恾帵偣傛丅(2) D(0) 傪恾帵偣傛丅 (3) D(t) 偑嬻偱側偔丆偐偮仮ABC偵娷傑傟傞傛偆側t偺斖埻傪媮傔傛丅 |
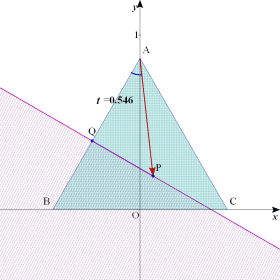 | 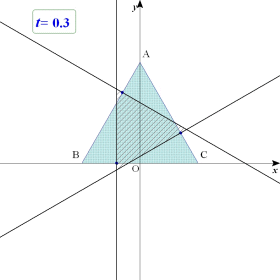 |