複素平面上における図形問題の解法には，様々な面白い要素を含んでいる。現行の課程では科目「数学B」の「複素数と複素数平面」において取り扱うことになっているが，機械的な計算によってその魅力を失わせている解法も目立つ。数学教育実践研究会の中村文則先生は，そうした複素数による図形変換を"作用素"としての観点からアプローチを試みた。研究会ではそのテーマを更に深め，分かりやすくイメージ化していったが，その内容が次のページにWeb化されている。
⇒「作用素としての複素数」
http://www.nikonet.or.jp/spring/thema/complex.htm
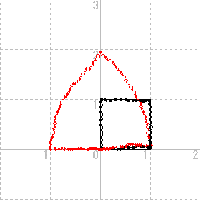
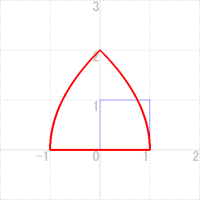
こうした複素変換を描画するのに十進BASICは最適である。それは独自の拡張機能として複素数モードを持っているからである。十進BASICではプログラムの序文に OPTION ARITHMETIC COMPLEX と宣言すると，複素数モードに設定される。そして，z=complex(x,y)でz=x+iyという複素数が得られ，w=z2と関数を定義するだけで変換後の複素数が得られる。その後Re(w)，Im(w)として，実部と虚部の部分を取り出し，描画すればよいわけである。1辺が1の正方形がw=z2でどのように変換されるかを，描画してみよう。正方形の辺をマウスペンで上手になぞっていくと，変換された図形が姿を現してくる。
 |  |  |
このようにして様々な複素変換をイメージ化していくとどうなるであろうか。それをまとめたのが次のページである。
⇒「複素変換で遊ぼう」
http://www.nikonet.or.jp/spring/cimg/cimg.htm
その中のいくつかを紹介したい。内容は難しくならないようにできるだけ数式を用いず，また，興味を持たせるために身近な絵を用いるようにした。
最も大きな特徴はマウスペンで"なぞる"ことで，変換後の図形が姿を現すため，シミュレーションとしての価値が大きいことである。次の図はw=z2で家，車，象それぞれを変換して得られた図である。
 |  |  |
変換の関数を変えて試してみよう。いくつかの例を次に挙げておく。
 |  |  |
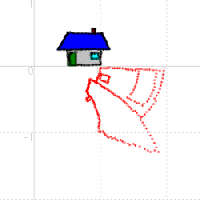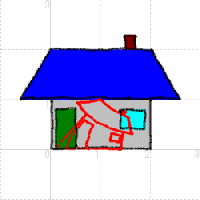| w=1/z の変換 | w=√z の変換 | w=ez の変換 |
さてこのような変換をどのように説明すればよいであろう。数式で押していくと，興味あふれる題材を無味乾燥なものにしてしまう。そこでこうした説明についてもイメージ化してしまおう。
変換 w=z2 を例にとって考えてみる。z=x+yi とし，次の図のように，家の図の横の線を作っているy=0,1,2の3本の直線を変換してみる。同様にx=−1,0,1の3本の直線も変換する。
すると原点を焦点，実軸を軸とする放物線が現れてくる。実は今まで直線で書かれていた図が，今度は放物線にそって描かれていくことになるのである。
 |  |  |
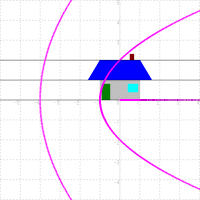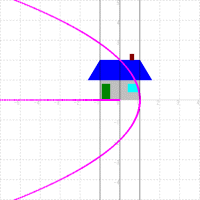| 水平な直線を変換 | 垂直な直線を変換 | 変換された直線を合成 |
同様にして変換する関数を変えてみると，次のようになる。
 |  |  |
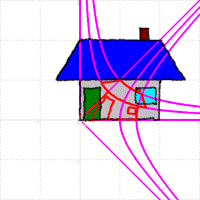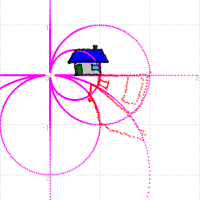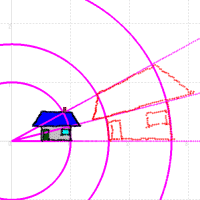| w=√z の変換 | w=1/z の変換 | w=ez の変換 |
様々な図形を複素変換をイメージ化してきたが，平面全体を変換するとどうなるかをみてみよう。
 | ⇒ |  |
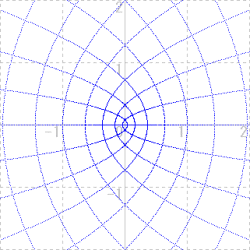実軸に平行な直線と平行な直線全体を変換してみる。次の図は w=z2で変換したものである。先ほど見たように，原点を焦点とし，実軸を軸とする放物線の集合となっているのがわかる。
他の変換ではどうであろうか。代表的なものを見てみよう。
 |  |  |
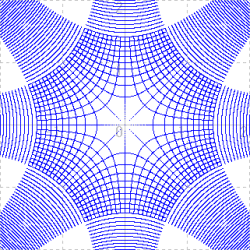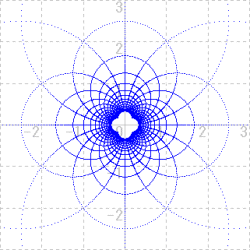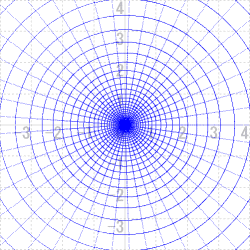| w=√z の変換 | w=1/z の変換 | w=ez の変換 |
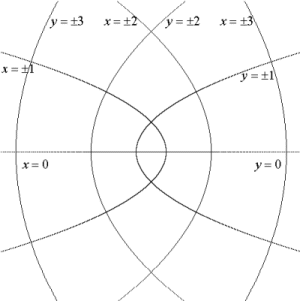
これらの複素変換の特徴は，任意の2つの曲線のなす角が変換後も等しく保たれている点である。2つの曲線のなす角とは，交点でそれぞれの曲線に接線を引いたとき，その接線のなす角をいうが，この様な変換を「等角写像」という。直行座標を変換したので変換後の曲線のなす角は，どれも90°になっているのがわかる。
 |  |
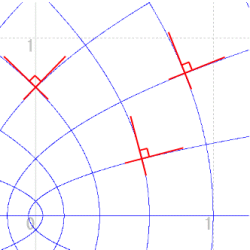座標平面全体を変換して新しい座標系を作ったわけであるが，新しい座標系があれば最初からそこに図形を書き込んでいくこともできる。変換w=z2で考えてみよう。次の左の図が変換された新しい座標系で，そこに右の座標を持つ家を描画してみよう。
 |  |
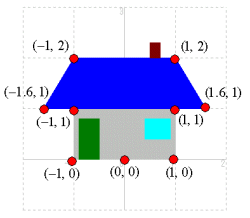元の図の点の座標に対応する新しい座標系の点をプロットする。プロットされた点を丁寧になぞっていくのである。（w=z2の変換は原点が原点に移されるので注意しなければならない。）
 |  |
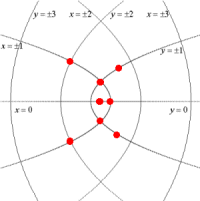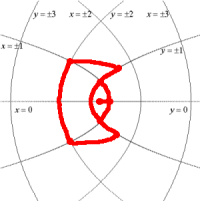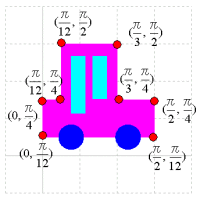
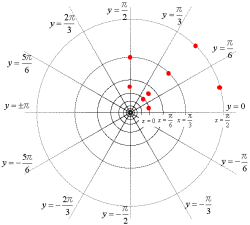
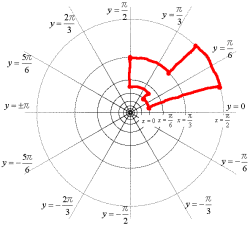
このように基底を変換することで，図形を簡単に描くことができる。新たな座標系を生徒に与えれば，手作業で図形の複素変換を実感できることになる。つまり，複素変換という難解な題材が，より身近に親しみやすい題材へと変えていくことができるのである。次の図はw=ezについて新しい座標系に車の図を描いたものである。
 |  |  |