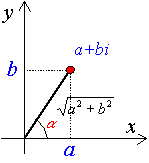
複素数 x+y iを平面上の点(x，y)で表わすことを考えます。このように複素数を表わすのに使われる平面をガウス平面といいます。ガウス平面でx軸上の点は実数を表わし、y軸上の点はy iという形の純虚数を表わします。

　いま、ある複素数 x+y i に a+b iという複素数をかけ、u+v iという複素数になったとします。つまり、

　　u+v i=(a+b i)(x+y i)
　　　　=(ax-by)+(bx+ay) i

　これより
　　･･･(1)

式(1)は

　　･･･(2)

という1次変換と同じであることを示しています。

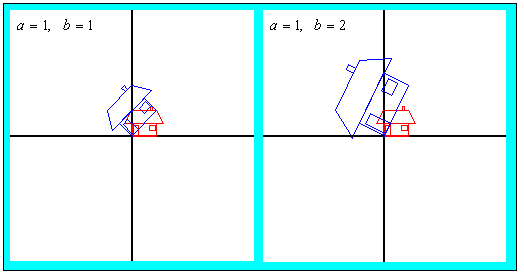
　この変換は、右の図のように角αだけ回転し、倍に拡大するという変換を表わしています。

　

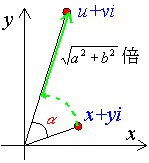
　つまり、複素数 x+yiにある複素数 a+b i をかけるということは、回転と拡大の合成変換になっているのです。