【TOP】【BACK】【NEXT】

■■　テーマ～シミュレーションとしての利用　■■

　Grapesなど関数描画ソフトでは，シミュレーションし難いものをGCでシミュレートしてみよう．その際には，所定の図形を作図するため補助線を利用する必要が出てくる．また，必要に応じてその補助線を非表示にすることで所期の目的を達成することになる．

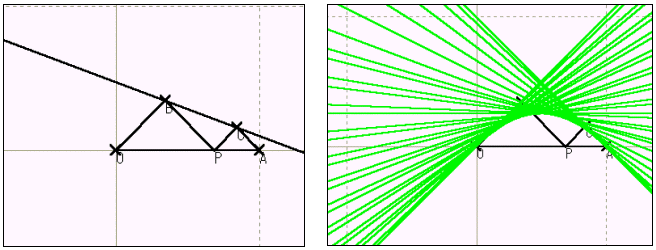
《演習３》2点A(1 , 0)，O(0 , 0)を両端とする線分上の任意の点をＰとする．OP，PAを斜辺とする直角二等辺三角形を線分OAの上方に作り，頂点をB,Cとする．このとき，直線BCが通らない範囲を求めよ． （法政大）

　解答としては，P(t , 0) (0＜t＜1)とおき，直線BCの方程式をtの2次方程式とみて0＜t＜1に実数解をもつ条件から，直線BCの通過領域を導き出す問題である．しかし，これほど図形的な問題であればそのままの状態でシミュレートしてみたい場面でもある．
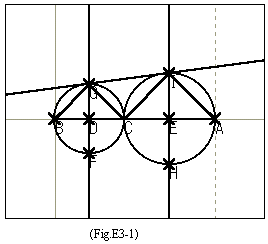
　この問題で，私が使った補助線は以下のとおりである．もっと間単にできるかもしれないが参考として皆さん各自で挑戦をしていただきたい．

＜以下の頂点は，Fig.E3-1による＞

  1. A(1 , 0)，B(0 , 0)の２点をとる
    　※[作図]→[点]→[xy座標を与える]
  2. 線分ABを描く
    　※[作図]→[線分･多角形]→[2点を結ぶ線分]
  3. 線分AB上に1点をとる
    　※[作図]→[点]→[新しい点の追加]

    《直角三角形BCGの描画》

  4. 線分BCの中点Dをとる
    　※[作図]→[分点]→[n等分](n=2)
  5. 点Dを通りABに垂直な直線を引く
    　※[作図]→[直線]→[直線に垂直1点を通る]
  6. 点Dを中心として点Bを通る円を描く
  7. ⑤⑥の直線と円の交点をとる
    　※[作図]→[点]→[交点] →[直線と円]

　直角三角形ACIについても同様に描画してから，直線GIを引き(Fig.E3-1)を得る．
　あとは点の名前を変更後，不必要な点や円の'色'を'書かない'に設定して(Fig.E3-2)を得る，直線の軌跡を設定してシミュレーションをすることになる．(Fig.E3-3)

【TOP】【BACK】【NEXT】