 丂偙偺栤戣偱偼丆摨堦尫偵懳偡傞俀偮偺墌廃妏傪偲傝偦傟偑摍偟偄偲偄偆偩偗偱偼乽偩偐傜壗側偺丠乿偲偄偆掱搙偱丆妛廗岠壥偼掅偄(Fig.E1-1)
丂偙偺栤戣偱偼丆摨堦尫偵懳偡傞俀偮偺墌廃妏傪偲傝偦傟偑摍偟偄偲偄偆偩偗偱偼乽偩偐傜壗側偺丠乿偲偄偆掱搙偱丆妛廗岠壥偼掅偄(Fig.E1-1)|
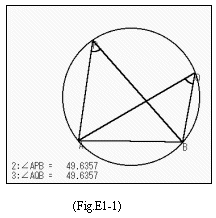
乻墘廗侾乼仢僥乕儅乽墌廃妏偺掕棟偺媡乿偺妋擣掕拝 係揰A,B,P,Q偵偮偄偰丆P,Q偑摨偠懁偵偁偭偰佢APB=佢AQB側傜偽偙偺係揰偼摨堦墌廃忋偵偁傞 |
 丂偙偺栤戣偱偼丆摨堦尫偵懳偡傞俀偮偺墌廃妏傪偲傝偦傟偑摍偟偄偲偄偆偩偗偱偼乽偩偐傜壗側偺丠乿偲偄偆掱搙偱丆妛廗岠壥偼掅偄(Fig.E1-1)
丂偙偺栤戣偱偼丆摨堦尫偵懳偡傞俀偮偺墌廃妏傪偲傝偦傟偑摍偟偄偲偄偆偩偗偱偼乽偩偐傜壗側偺丠乿偲偄偆掱搙偱丆妛廗岠壥偼掅偄(Fig.E1-1)
|
 (夵椙1) 墌傪"彂偐側偄"偱丆揰Q傪"僼儕乕"偵摦偐偣傞傛偆偵偡傞丏
(夵椙1) 墌傪"彂偐側偄"偱丆揰Q傪"僼儕乕"偵摦偐偣傞傛偆偵偡傞丏
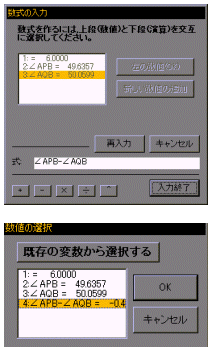
(夵椙俀) 佢APB=佢AQB偲側傞揰傪婳愓偱昞尰偟偰丆扵偝偣偰傒傞丏
丂仸[應掕]仺[悢幃]乮佢APB-佢AQB傪愝掕乯
丂仸[婳愓]仺[愝掕]仺[曄悢](佢APB-佢AQB傪慖戰)
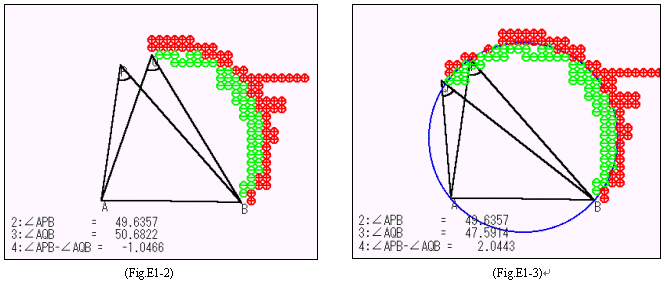
| 乻墘廗俀乼(墘廗侾)偺庤朄傪巊偭偰丆乽俀揰A,B偐傜偺嫍棧偺斾偑AP:BP=2:1偲側傞揰偺婳愓乿傪峫偊偝偣傞 嫵嵽傪嶌惉偟偰傒傛偆 |