【TOP】【BACK】【NEXT】
(3)複素数に関する教材〜複素数変換も簡単
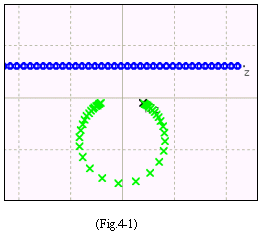 【例題4】 w=1/zによる変換で複素数zはどう変換されるか
【例題4】 w=1/zによる変換で複素数zはどう変換されるか
(準備)
- 座標倍率を複素数用に設定
※[ズーム]→[複素数用]
- 新しい点をとり名前をzとする
※[編集]→[点](点Aを選択)→('名前'を'z'に)
- 点1/zをとり,名前を'1/z'にする
※[作図]→[複素数]→逆数(1/z)
- 2点の軌跡を設定
(Step1)
- 「点zが直線上を動くときの像1/zの軌跡は」
(ア)直線が原点を通らないとき
(イ)直線が原点を通るとき
- 「点zが,円周上を動くときの像1/zの軌跡は」
(ア)原点が円の外部にある場合
(イ)原点が円の内部にある場合
(ウ)原点を通る場合
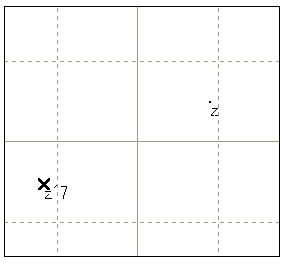 【例題5】方程式 の解を探す
【例題5】方程式 の解を探す
(準備)
- 座標倍率を複素数用に設定
※[ズーム]→[複素数用]
※[オプション]→[座標系の種類]→[極座標]
- 新しい点をとり名前をzとする
※[編集]→[点](点Aを選択)→('名前'を'z'に)
- 点 をとり,名前を'z^7'にする
※[作図]→[複素数]→[^(べき)](数値7)
(Step1)
- 「点zを動かして点z^7が点1に重なるようにしてみよう」
※zの位置とz^7にはどんな関係があるか
- 「単位円を作ってその円周上を動かしてみよう」
※原点をとる [作図]→[点]→[その他]→[xy座標を与える](数値を指定x←0,y←0)
※[Shift]を押しながら点zを動かすと近接した単位円上を動く
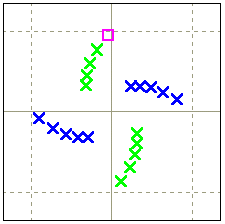 【例題6】点zをとり,z^2,z^3,z^4,…,z^10の9個の点をとる.
【例題6】点zをとり,z^2,z^3,z^4,…,z^10の9個の点をとる.
奇数冪を青,偶数冪を緑に設定して次のようにするには点zをどの位置にすればよいか?またそれは何箇所あるか?
(Step1)
- 全てが重なる
- 2群に分ける
- 5群に分ける
以上で【例題】は終了です.ここからは皆さん自身でGCを楽しんでください.そのために基本的作図練習の問題も含めて何題か演習問題を作っておきました.
【TOP】【BACK】【NEXT】
 【例題4】 w=1/zによる変換で複素数zはどう変換されるか
【例題4】 w=1/zによる変換で複素数zはどう変換されるか 【例題4】 w=1/zによる変換で複素数zはどう変換されるか
【例題4】 w=1/zによる変換で複素数zはどう変換されるか 【例題5】方程式 の解を探す
【例題5】方程式 の解を探す 【例題6】点zをとり,z^2,z^3,z^4,…,z^10の9個の点をとる.
【例題6】点zをとり,z^2,z^3,z^4,…,z^10の9個の点をとる.