戞俆係夞杒奀摴嶼悢悢妛嫵堢夛 嶥杫戝夛 崅摍妛峑晹夛
戞俆暘壢夛 嫵嬶丒僐儞僺儏乕僞乽幚尡(幚尒)揑悢妛偺偡偡傔乿
乣恎嬤側慺嵽傪棙梡偟傛偆乣
丂2師娭悢偺巜摫傪拞怱偵嶥杫憯娾崅摍妛峑丂丂悰丂尨丂丂枮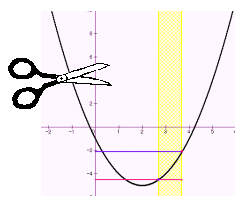 丂
丂
!偼偠傔偵
丂乽僥儗價僎乕儉悽戙乿偲偄偆尵梩偑巰岅偵姶偠傜傟傞傎偳偺惃偄偱巕嫙偨偪偺廃傝偵偼丆僷僜僐儞偺傒側傜偢忣曬婡婍偑偛偔帺慠偵堨傟偰偄傞丏嵟怴偺僥儗價僎乕儉偵偍偗傞夋憸偺儕傾儕僥傿偼杮摉偵慺惏傜偟偄傕偺偱偁傞丏俁D夋憸側偳偼傑傞偱幚幨偲媈偆傎偳偺弌棃忋偑傝偵側偭偰偄傞丏搊応恖暔偑僎乕儉婡偺拞偱"惗偒偰偄傞"偲偄偭偨曽偑揔愗偐傕偟傟側偄丏壖憐尰幚偲尰幚悽奅偑巕嫙偨偪偺怱徾偺悽奅偱僷儔儗儖偵恑峴偟偦偺嫬奅偑崱幐傢傟偮偮偁傞丏丂嶐擭偼乽嫵幒偵帇妎悢妛傪両乿偲偄偆僥乕儅偱Grapes側偳僼儕乕僜僼僩傪巊偭偰嫵嵽偺僀儊乕僕壔傪恾傞儗億乕僩傪敪昞偝偣偰偄偨偩偄偨丏
丂杒悢嫵慡摴戝夛傕崱擭偱俆係夞栚傪寎偊丆崱擭偐傜戞俆暘壢夛偺柤徧偑乽嫵堢岺妛乿偐傜乽嫵嬶丒僐儞僺儏乕僞乿偵堦怴偝傟偨丏"嫵嬶"偲偄偆柤徧偑慜柺偵弌偰偒偰偄傞埲忋偦傟偵偮偄偰偺儗億乕僩偑偁偭偰傕傛偄偱偁傠偆丏杒悢嫵偱偺敪昞偵偍偄偰嫵嬶偲偄偭偰傑偢晜偐傇偺偼娭悢嫵嵽偱偺"僽儔僢僋儃僢僋僗"偱偁傠偆偐丏嶐擭偺島廗夛偵偍偗傞戝嶳惸愭惗(摉帪嶥杫搶崅峑)偺擬怱側島墘傪巚偄弌偡丏傑偨丆棷朑戝夛偱偼攱惗揷寬愭惗(摉帪棷朑崅峑)偑丆庤嶌傝偺僒僀僐儘傪巊偭偨妋棪偺庼嬈偵偮偄偰偺敪昞側偳慺惏傜偟偄傕偺偱偁偭偨丏
 丂崱夞偺敪昞偺僥乕儅偼"偱偒傞偩偗庤娫傪偐偗偢偵帇妎壔偟偨庼嬈"偱偁傞丏崱擭搙偺庼嬈偐傜乽俀師娭悢偺嵟戝抣丒嵟彫抣偺墳梡乿傪拞怱偵敪昞偝偣偰偄偨偩偔丏傑偨丆応崌暘偗偺僔僃乕儅偵偮偄偰偼嶥杫怴愳崅峑 拞懞暥懃愭惗偺悢幚尋偱偺敪昞傪慡柺揑偵巊傢偣偰偄偨偩偄偨丏
丂崱夞偺敪昞偺僥乕儅偼"偱偒傞偩偗庤娫傪偐偗偢偵帇妎壔偟偨庼嬈"偱偁傞丏崱擭搙偺庼嬈偐傜乽俀師娭悢偺嵟戝抣丒嵟彫抣偺墳梡乿傪拞怱偵敪昞偝偣偰偄偨偩偔丏傑偨丆応崌暘偗偺僔僃乕儅偵偮偄偰偼嶥杫怴愳崅峑 拞懞暥懃愭惗偺悢幚尋偱偺敪昞傪慡柺揑偵巊傢偣偰偄偨偩偄偨丏
丂帇妎揑側庼嬈揥奐傪峫偊偨偲偒偵朰傟偰側傜側偄揰偼丆嫵嵽嶌惉偵偐偐傞弨旛帪娫偲慺嵽偺擖庤偺偟傗偡偝偱偁傠偆丏偳傫側偵桪傟偨嫵嵽揥奐傕偦偺弨旛偵朿戝側帪娫偲楯椡偑偐偐傟偽枅擔偺嶨柋偵捛傢傟傞崅峑嫵巘偵偲偭偰偼恏偄擔乆偲側傞丏
丂娙曋惈傪儌僢僩乕偲偟偨偨傔嫵嬶偲偟偰偼抰愘側傕偺偱偼偁傞偑丆巊偭偰偙偦偺嫵嬶偱偁傞丏偳傫側偵娙扨側嫵嬶偱傕崟斅偲僠儑乕僋偺庼嬈偲偼堘偭偨岠壥偑婜懸偱偒傞丏嶲壛偝傟偨彅愭惗偵偄偔傜偐偱傕嶲峫偵側傟偽岾偄偱偁傞丏
仭仭仭 俀師娭悢偺嵟戝抣丒嵟彫抣乣僴僒儈偲巻 仭仭仭
俀師娭悢偺嵟戝抣丒嵟彫抣偵娭偡傞栤戣偼丆師偺傛偆偵暘椶偱偒傞丏- 掕媊堟偺惂尷側偟
椺侾乯y=-2x2+3x-5 偺嵟戝抣丒嵟彫抣偑偁傟偽媮傔傛丏傑偨偦偺偲偒偺x偺抣傕媮傔傛丏 - 掕媊堟偺惂尷偁傝
丂嘆娭悢丒嬫娫偲傕偵屌掕
丂丂椺俀乯y=x2-2x-2 偺嵟戝抣丒嵟彫抣偲偦偺偲偒偺x偺抣傪媮傔傛丏
丂嘇嬫娫偺堦抂偑曄壔
丂丂椺俁乯a傪惓偺掕悢偲偡傞偲偒丆0亝x亝a 偵偍偗傞娭悢y=x2-4x-1 偺嵟戝抣偲嵟彫抣傪媮傔傛丏
丂嘊嬫娫偺椉抂偑曄壔
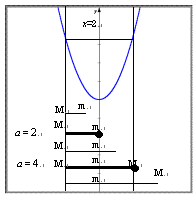
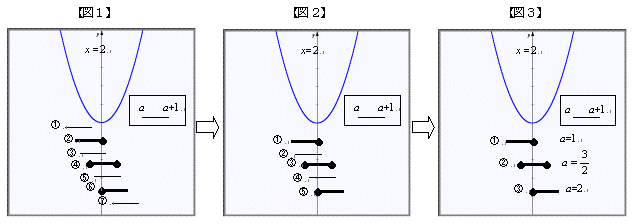
丂丂椺係乯俀師娭悢y=x2-4x-1 偺a亝x亝a+1偵偍偗傞嵟彫抣傪m(a)丆嵟戝抣M(a) 偲偡傞丏
丂丂丂偙偺偲偒丆m(a)丆M(a) 傪a偺幃偱昞偣丏
丂嘋娭悢偑曄壔
丂丂椺俆乯2師娭悢 y=x2-2ax-1 偺0亝x亝6 偵偍偗傞嵟戝抣偲嵟彫抣傪媮傔傛丏
|
丂崱擭搙偺庼嬈偱偼偙偺暘椶偵廬偄丆巜摫弴彉傕忋婰偺棳傟偱峴偭偰傒偨丏巜摫偵偁偨偭偰棷堄偟偨揰偼埲壓偺捠傝偱偁傞丏
仧仧 摦偒傪敽偆嫵嵽偺帇妎壔乮嫵嬶偲僔僃乕儅偺妶梡乯仧仧丂暯峴堏摦偺偲偒側偳僌儔僼傪摦偒偑梸偟偄応柺偑偁傞丏摦偒慡懱傪採帵偡傞応崌丆捀揰側偳堦揰偵拝栚偝偣傞応崌偑偁傞丏僷僜僐儞偵傛傞僔儈儏儗乕僔儑儞傕峴偭偰偒偨乣H10敪昞儗億乕僩乽嫵幒偵帇妎揑悢妛傪乿乣偑丆崱擭搙偼A3斉偺梡巻丒僴僒儈丒帴愇傪嫵幒偵帩偪崬傒庼嬈傪幚巤偟偰傒偨丏巻偱嶌偭偨曻暔慄偼"彂偒崬傒壜擻","堏摦丒屌掕偑梕堈"側偳棙揰偑懡偄丏側偵傛傝傕弨旛偺庤寉偝偑堦斣偱偁偭偨丏
亂鶤乗嘇偺巜摫椺亃
- 梡堄偟偨A3偺巻偵曻暔慄傪彂偄偰偍偔丏崟斅曽岦偵姫偄偰偍偒嵍抂傪帴愇偱屌掕偡傞丏姫偄偰偁傞晹暘傪栠偟梡堄偟偨A3偺巻偵曻暔慄傪彂偄偰偍偔丏崟斅曽岦偵姫偄偰偍偒嵍抂傪帴愇偱屌掕偡傞丏姫偄偰偁傞晹暘傪栠偟偰曅抂傪曄摦偝偣丆嵟彫抣偺曄傢傝栚傪妋擣偡傞丏
仸嶥杫堫塤崅峑 戝壨撪愭惗偺幚慔偱偼柾憿巻傪梡偄偰峴偭偰偄偨丏柾憿巻偺曽偑埑搢揑偵尒傗偡偔岠壥偑崅偄偙偲偼尵偆傑偱傕側偄丏 - 慜崁偱僔儈儏儗乕僔儑儞傪偟偨屻丆僔僃乕儅傪梡偄偨夝愢傪峴偆丏
丂惗搆偵偼塃偺僔僃乕儅傪梡偄偰嵟戝抣丒嵟彫抣偺曄傢傝栚偺昞尰傪偡傞傛偆巜摫偡傞丏
丂偙偺恾傪偡偖採帵偡傞偺偱偼側偔丆嵟戝抣M丆嵟彫抣倣偦傟偧傟偺応崌偵偮偄偰峫嶡偟塃恾偵偄偨傞丏
丂懢慄晹偑偦傟偧傟偺曄傢傝栚偲側傝丆塃抂偺抣傛傝曄傢傝栚偺a偺抣傪尒偰庢傟傞傛偆偵偡傞丏丂僔僃乕儅偺壓偵a偵娭偡傞悢捈慄傪昤偒丆廲偵暘妱偟応崌暘偗傪偟偰夝摎偡傞丏
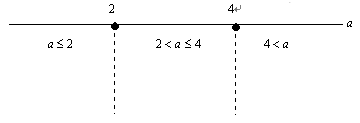 丂嘊偲嘋偼掕媊堟偺嬫娫暆偑摍偟偄揰偱丆摨條偺梫慺傪娷傫偱偄傞丏惗搆偐傜尒傞偲"応崌暘偗"偺棈傫偩栤戣偼嬯庤偲偡傞孹岦傕曄傢傜側偄丏偙偙偱傕A3巻傪巊偭偰娙扨側僔儈儏儗乕僔儑儞傪偟偰傒傛偆丏
丂嘊偲嘋偼掕媊堟偺嬫娫暆偑摍偟偄揰偱丆摨條偺梫慺傪娷傫偱偄傞丏惗搆偐傜尒傞偲"応崌暘偗"偺棈傫偩栤戣偼嬯庤偲偡傞孹岦傕曄傢傜側偄丏偙偙偱傕A3巻傪巊偭偰娙扨側僔儈儏儗乕僔儑儞傪偟偰傒傛偆丏
丂巜摫弴彉偼嘋傪僌儔僼偵帇揰傪堏偡偙偲偵傛傝嬫娫堏摦宆偺嘊偺峫偊偱尒傞偙偲偐傜嘊仺嘋偲偡傞丏亂鶤乗嘊偺巜摫椺亃
- 嘊偺椺戣傪採帵偡傞丏偦偺屻偍傕傓傠偵巻偲偼偝傒傪庢傝弌偟丆A3巻偺巻愗傝傪巒傔傞丏
丂傑偢丆曻暔慄傪愗傝弌偡丏偙傟偵幉傪愒僠儑乕僋偱彂偒崬傒崟斅偵帴愇偱屌掕偡傞丏師偵丆傕偆1枃偺A3巻偐傜挿曽宍偺憢傪愗傝庢傝丆愗傝庢偭偨晹暘偺椉懁偺廲慄晹暘偵a丆a+1偲嬫娫偺椉抂偺抣傪彂偒崬傓丏埲忋偱弨旛姰椆偱偁傞丏
丂傑偢嵟戝抣偵拝栚偝偣崟斅偵屌掕偝傟偨曻暔慄偺忋偵巻傪偐傇偣備偭偔傝偲嵍塃偵堏摦偝偣傞丏偙傟偩偗偱偁傞丏偁偲偼丆偙傟偵帺暘側傝偺墘媄傪怐傝岎偤側偑傜"曄傢傝栚"傪峫偊偝偣傞丏
丂嵟戝抣偼曄摦偟側偑傜傕嬫娫撪偱偺嵟戝抣傪曐帩偟偰偄傞揰偑棟夝偝傟傟偽廩暘偱偁傠偆丏
丂師偵嵟彫抣傕摨條偱偁傞丏壗偱傕側偄傛偆偩偑丆撍慠偵巻偲偼偝傒傪庢傝弌偡巔偵乽壗偺偮傕傝偩傠丠乿偲偙偪傜偵拲堄偑廤拞偡傞岠壥傕庤揱偭偰惗搆偺棟夝偼忋乆偱偁偭偨丏 - 嘇偲摨條偵僔儈儏儗乕僔儑儞偑廔傢偭偨傜僔僃乕儅傪梡偄偰峫嶡偡傞丏僥乕儅偼"徣椡壔"偱偁傞丏応崌暘偗偺悢偩偗恾傪彂偔偺偼戝曄偱偁傞丏
丂惗搆偑巚峫偡傞嵺偵棙梡偡傞僔僃乕儅傕峀偄堄枴偱偼嫵嬶偺堦偮偲峫偊傜傟傞丏嫵嵽棟夝傪曗彆偡傞傕偺偼慡偰嫵嬶偲峫偊偰偄傞丏崱擭搙偺庼嬈偱偼忋婰嘊嘋偺巜摫偵偁偨偭偰怴愳崅峑拞懞愭惗偺悢幚尋偵偍偗傞儗億乕僩傪慡柺揑偵嶲峫偵偝偣偰偄偨偩偄偨丏
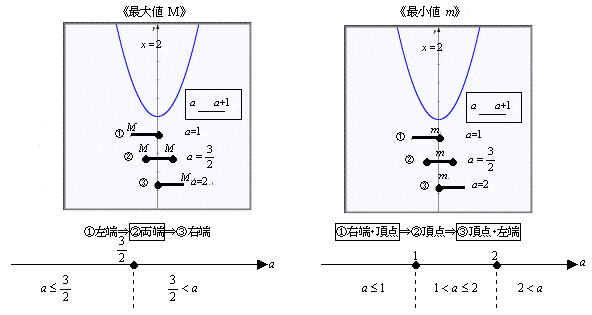
亂鶤乗嘋偺巜摫椺亃
- 嘊偼嬫娫偑堏摦偟偨偺偲偼堎側傝丆嘋偼嬫娫偼屌掕偝傟偰偄傞偑僌儔僼偑堏摦偡傞応崌偱偁傞丏
丂偙偙偱傕愭傎偳愗傝弌偟偨曻暔慄偲嬫娫憢偺A3巻傪巊偭偰僔儈儏儗乕僔儑儞傪偡傞丏
丂偙偙偱傕嵟戝抣丆師偵嵟彫抣偲曅曽偢偮峫偊偝偣傞偲傛偄丏
丂慜夞偲棤曉偟偰嬫娫憢偺曽傪崟斅偵屌掕偟丆嬫娫偺椉抂偺抣傪彂偒崬傓丏偦偺嵺丆椉懁偺嬫娫奜偺晹暘傪廲愜傝偟偰偍偔偲丆僔儈儏儗乕僔儑儞拞嬫娫憢偑愜傟嬋偑偭偰偙側偄丏曻暔慄巻傪嬫娫憢偺棤懁偵嵎崬傫偱備偭偔傝偲嵍塃偵堏摦偝偣傞丏嵟戝抣偼曄摦偟側偑傜傕嬫娫撪偱偺嵟戝抣傪曐帩偟偰偄傞揰偑棟夝偝傟傟偽廩暘偱偁傠偆丏師偵嵟彫抣傕摨條偵僔儈儏儗乕僔儑儞偡傞丏
丂偙偙偱堦搙庤傪巭傔偰丆僔僃乕儅偺峫嶡偵堏傞丏曻暔慄巻偲嬫娫憢偼帴愇偱屌掕偟偰偍偔丏 - 崱夞傕僥乕儅偼"徣椡壔"偱偁傞丏応崌暘偗偺悢偩偗恾傪彂偔偺偼戝曄偱偁傞丏
丂摿偵僌儔僼偑堏摦偡傞偲偄偆偙偲偱嘊傛傝傕恾傪彂偒偵偔偄丏嵟戝抣丒嵟彫抣偺堦曽傪昞尰偡傞偲偟偰傕偦傟偧傟俁捠傝傎偳偺恾傪昤偐偹偽側傜側偄丏乽壗偐徣椡壔偺椙偄岺晇偼側偄偐丠乿側偳偲敪栤偟偰傒傞丏偦偺嵺丆僸儞僩偼愭傎偳偺僔儈儏儗乕僔儑儞偵偁傞丏
丂偙偙偱丆愭傎偳偺曻暔慄巻偲嬫娫憢偵嵞搙搊応偟偰傕傜偆丏
丂崱搙偼丆曻暔慄巻傪屌掕偟偰嬫娫憢傪摦偐偟偰傒傞丏帇揰傪偳偪傜偵屌掕偡傞偐偺堘偄偺傒偱尰徾揑偵偼摨條偱偁傞偙偲偑尒偰庢傟傞丏
丂偡側傢偪嘊偱巊偭偨僔僃乕儅偼丆傎傫偺彮偟偺夵椙偱巊梡偱偒傞丏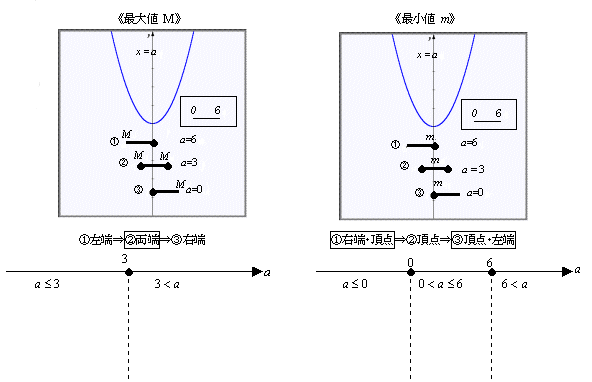
丂崱夞偼嶥杫怴愳崅峑 拞懞暥懃愭惗偺悢幚尋偵偍偗傞敪昞傪庼嬈偵慡柺揑偵棙梡偝偣偰偄偨偩偄偨丏偙傟傑偱偺悢幚尋傗杒悢嫵偱悢懡偔偺慺惏傜偟偄儗億乕僩傪敪昞偝傟偰偄傞拞懞愭惗偩偑丆巹偼亀彫庤媄亁僔儕乕僘偺僼傽儞偺堦恖偱偁傝丆偙偺儗億乕僩傕亀彫庤媄僔儕乕僘亁偺幚慔曇偲尵偭偨偲偙傠偱偁傞丏姶幱両
乻嶲峫儗億乕僩乼亀擇師娭悢偺嵟戝嵟彫栤戣偺偪傚偭偲偟偨彫庤媄亁
嶥杫怴愳崅峑 拞懞暥懃
亀嫵幒偵帇妎揑悢妛傪両乣悢妛梡僼儕乕僜僼僩僂僃傾傪棙梡偟偨嫵嵽嶌惉椺亁
嶥杫憯娾崅摍妛峑丂悰尨丂枮
 丂
丂
 丂
丂
 丂崱夞偺敪昞偺僥乕儅偼"偱偒傞偩偗庤娫傪偐偗偢偵帇妎壔偟偨庼嬈"偱偁傞丏崱擭搙偺庼嬈偐傜乽俀師娭悢偺嵟戝抣丒嵟彫抣偺墳梡乿傪拞怱偵敪昞偝偣偰偄偨偩偔丏傑偨丆応崌暘偗偺僔僃乕儅偵偮偄偰偼嶥杫怴愳崅峑 拞懞暥懃愭惗偺悢幚尋偱偺敪昞傪慡柺揑偵巊傢偣偰偄偨偩偄偨丏
丂崱夞偺敪昞偺僥乕儅偼"偱偒傞偩偗庤娫傪偐偗偢偵帇妎壔偟偨庼嬈"偱偁傞丏崱擭搙偺庼嬈偐傜乽俀師娭悢偺嵟戝抣丒嵟彫抣偺墳梡乿傪拞怱偵敪昞偝偣偰偄偨偩偔丏傑偨丆応崌暘偗偺僔僃乕儅偵偮偄偰偼嶥杫怴愳崅峑 拞懞暥懃愭惗偺悢幚尋偱偺敪昞傪慡柺揑偵巊傢偣偰偄偨偩偄偨丏